Константа - холл
Cтраница 2
Отсюда следует, что поскольку в кристаллах могут быть носители двух знаков, то и знак константы Холла может быть различен; и зависит от того, чей эффект преобладает - электронов или дырок. Объяснение существования обоих знаков постоянной Холла было крупным достижением квантовой теории переноса, убедительно доказавшей справедливость представлений о состояниях, электронов в периодическом поле кристалла. [16]
Энергия однократной ионизации примеси междуузельного цинка измерялась по наклону прямой на графике зависимости логарифма проводимости ( или константы Холла) от обратной температуры; она составляет несколько сотых электрон-вольта, примерно 0 04 эв. На основании сказанного выше можно предположить, что при столь низких температурах играют роль только объемные процессы, и энергия активации 0 04 эв представляет собой истинно объемные свойства. [17]
Первый из них измерял температурную зависимость электропроводности окиси цинка ( подвергнутой спеканию и в виде напыленных слоев), а также константу Холла при 25 и - 190 С. Наклон, который дает энергию ионизации доноров, уменьшается с ростом проводимости - в приближенном согласии с правилом Мейера 30 ] для окисных полупроводников. Энергия ионизации падает с увеличением концентрации донорного междуузельного цинка. [18]
 |
Эффект Холла в электронном полупроводнике.| Эффект Холла в дырочном полупроводнике. [19] |
Может оказаться, что ток одновременно переносится и электронами и дырками. В таких случаях константа Холла зависит от разности обоих токов, тогда как в величине электропроводности они складываются. Уравнения ( 13) и ( 14) в этом случае уже не имеют места и заменяются другими. В частности, эффект Холла может оказаться равным нулю, хотя и подвижность электронов и подвижность дырок, каждая в отдельности, велики. [20]
Это и есть холловское поле. Мы видим, что константа Холла обратно пропорциональна плотности электронов. [21]
Отсюда видно, что знак константы Холла совпадает со знаком заряда q частиц, обусловливающих проводимость данного материала. Поэтому на основании измерения константы Холла для полупроводника можно судить о природе его проводимости: если R 0, то проводимость электронная, если R 0, то дырочная. [22]
Хэррисон получил по существу одинаковые результаты как на монокристаллах, так и на спеченных образцах. Наклоны кривых зависимости логарифма константы Холла и логарифма проводимости от обратной температуры практически одинаковы. На разных образцах температурная зависимость подвижности одна и та же, но величина подвижности несколько изменяется от образца к образцу. [23]
Что называется константой Холла. У каких веществ - у проводников или полупроводников - константа Холла сильнее зависит от темпера - туры, почему. [24]
Обратим внимание на то, что эта величина зависит не только от плотностей электронов, но и от времени их свободного пробега. Выясним теперь, как ведут себя магнитосопротивление р и константа Холла R в области сильных магнитных полей. [25]
Так, Эпштейн и Вилди [61] утверждают, что определение константы Холла для термически обработанного полифталоцианина позволило сделать заключение о двух механизмах проводимости, проявляющихся в различных температурных интервалах. Наиболее достоверные результаты получены для полимеров на основе пирена и пиромеллитового диангидрида. Проводимость в этих полимерах дырочная. Многократные попытки обнаружить эффект Холла, предпринятые как в Институте полупроводников, так и другими исследователями, не привели к успеху. [26]
Таким образом, мы видим, что возникающая разность потенциалов пропорциональна величине магнитного поля и току через образец. Коэффициент пропорциональности Дх между Fx и Bz, Ix называется константой Холла, и, как видно, она определяется только концентрацией носителей тока. Когда вклад в проводимость обусловлен и электронами и дырками, выражение для постоянной Холла имеет более сложный вид. [27]
Система медь-палладий характеризуется большими отрицательными отклонениями при 1000 К, что согласуется с упорядочением ниже 600, где образуются сверхструктуры Cu3Pd и CuPd. В системе медь-никель имеются большие положительные отклонения при 1000 К, что можно согласовать с зависимостью константы Холла от состава и температуры для этих сплавов. [28]
Поверхностные уровни должны были бы в большей степени воздействовать на проводимость спеченных образцов, чем на константу Холла. Однако температурная зависимость последней точно такая же, как и для проводимости. [29]
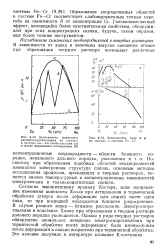 |
Зависимость удельного электросопротивления от состава ь системе Си - Аи после закалки ( а я после медленного охлаждения ( б.| Зависимость Ар / р и р от состава в системе Fe-Сг. [30] |
Страницы: 1 2 3