Кривая - плотность - распределение
Cтраница 1
Кривая плотности распределения при этом имеет симметричный вид. [1]
Кривая плотности распределения Коши ( рис. 2 - 1, а) с первого взгляда кажется очень похожей на кривую плотности нормального распределения, однако в действительности это совсем не так, ибо ее свойства резко отличны от свойств экспоненциальных распределений. Так, дисперсия отсчетов при таком законе распределения вероятностей принципиально не может быть указана, так как определяющий ее интеграл расходится. На практике это означает, что оценка дисперсии и с. Естественно, что использование такой оценки неправомерно. Четвертого момента ц у распределения Коши также не существует, так как определяющий его интеграл расходится, как и интеграл, определяющий дисперсию. [2]
Кривая плотности распределения на рис. 2 - 3 получена путем дифференцирования по б кривой распределения D, изображенной на рис. 2 - 1, и представляет собой истинную плотность распределения. [3]
Если кривая плотности распределения симметрична относительно среднего значения как, например в случае нормального распределения ( см. рис. 12.4), все центральные моменты нечетного порядка равны нулю. [4]
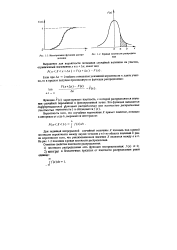 |
Интегральная функция распределения.| Кривая плотности распределения. [5] |
На рис. 1.2 показана кривая плотности распределения. [6]
Как видно из этого рисунка, кривая плотности распределения вероятностей для случайной величины, распределенной по нормальному закону, симметрична относительно значения х-т, называемого центром распределения. [7]
Как видно из этого рисунка, кривая плотности распределения вероятностей для случайной величины, распределенной по нормальному закону, симметрична относительно значения х т, называемого центром распределения. [8]
Как видно из этбго рисунка, кривая плотности распределения вероятностей для случайной величины, распределенной по нормальному закону, симметрична относительно значения х - т, называемого центром распределения. [9]
Любой капиллярно-пористый материал характеризуется видом так называемой кривой плотности распределения объемов пор по их размерам, представленной в качестве примера на рис. 1.8. Некоторые материалы обладают пористой структурой с двумя максимумами на кривой распределения по размерам. [10]
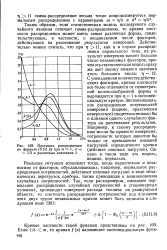
Обозначим этот момент через t 1 и построим кривую плотности распределения параметра ( фиг. Кривая оказывается слегка сдвинутой в сторону нижнего допуска и размах распределения стал шире. [11]
Обозначим этот момент через t 1 и построим кривую плотности распределения параметра ( фиг. Кривая оказывается слегка сдвинутой в сторону нижнего допуска и размах распределения стал шире. [12]
Очевидно, что с увеличением среднего квадратического отклонения ах максимум уменьшается и кривая плотности распределения растягивается вправо я влево от точки тх одинаковым образом. С уменьшением значения ах, она, напротив, прижимается к вертикальной прямой. [13]
 |
Плотность распределения. [14] |
Таким образом, если статистическая модель исследуемого случайного явления отвечает гамма-распределению, то кривая плотности распределения может иметь самые различные формы, свидетельствующие, в частности, о неодинаковом числе факторов, действующих на рассеивание результатов измерений. [15]
Страницы: 1 2 3