Кривая - плотность - вероятность
Cтраница 1
 |
Гистограмма н кривая плотности вероятностей. [1] |
Кривая плотности вероятностей f ( x) хорошо совмещается с гистограммой. [2]
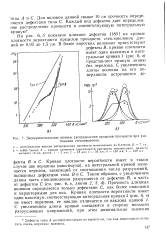 |
Экспериментальные кривые распределения пределов прочности при растяжении стекловолокон. [3] |
Кривая плотности вероятности имеет в таком случае две вершины ( максимума), на интегральной кривой намечается перелом, зависящий от соотношения числа разрушений, вызванных дефектами типа В и С. Прочность длинных волокон определяется только дефектами С, как более опасными и характерными для них. [4]
Кривая плотности вероятности симметрична относительно математического ожидания. [5]
Кривая плотности вероятностей случайной величины т ] а - является зеркальным отражением логнормальной кривой распределения случайной величины от вертикали, проходящей через точку у а. Распределение 1 - А, ( а - у; fj, cr2) в отличие от классического логнормального распределения характеризуется отрицательной асимметрией. [6]
Кривая плотности вероятности нормального распределения симметрична относительно максимальной ординаты. [7]
Если кривая плотности вероятности имеет пологий левый и крутой правый спад, распределение имеет отрицательную асимметрию. В этом случае для показателей центра распределения имеем: математическое ожидание медиана мода. [8]
В случае, если кривая плотности вероятности имеет крутой левый и пологий правый спад, говорят, что распределение имеет положительную асимметрию. В этом случае координаты показателей центра распределения располагаются на оси абсцисс, как правило, следующим образом: мода медиана математическое ожидание. [9]
Закон распределения Кош и ( кривая плотности вероятностей приведена на рис. 2 - 1, а) важен для теории оценки погрешностей результатов измерений тем, что ему подчиняется, например, распределение отношения двух нормально распределенных центрированных случайных величин. [10]
Явление, состоящее в том, что кривая плотности вероятности имеет более толстые хвосты и более острый пик на среднем значении, чем это имеет место у нормального распределения. [11]
В этом случае имеется вероятность того, что кривая плотности вероятности скоростей ( соответствующих им частот) частиц не укладывается в выбранном диапазоне частот. [12]
Рассмотрим простейший опыт, в результате проведения которого можно получить кривую плотности вероятности по Гауссу. [13]
Полное решение этой задачи заключается, в установлении параметров, определяющих кривую плотности вероятности случайных отклонений отдельных мер от номинала. Эти отклонения являются случайными для совокупности мер и, в то же время, систематическими для каждой заданной меры. [14]
При изучении формы распределения случайной величины важно выяснить, симметрична ли относительно центра распределения кривая плотности вероятности. Показателем степени несимметричности этой кривой является безразмерная величина, называемая коэффициентом асимметрии. Коэффициент асимметрии обозначается как у или As. Рассмотрим на качественном уровне понятие асимметрии. [15]
Страницы: 1 2