Анализ - численный результат
Cтраница 1
Анализ численных результатов показал, что на промежутке времени 500 лет вековые возмущения большой полуоси ба, эксцентриситета бе и наклона 6z практически отсутствуют, в то время как угловые элементы в, Q и М претерпели значительные изменения из-за наличия вековых возмущений. [1]
 |
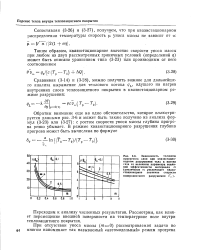
Коэффициенты интенсивности напряжения Fl п при одноосном и всестороннем растяжении плоскости с трехзвенной трещиной ветвления. [2] |
Анализ численных результатов позволяет заключить, что в случае задачи о ломаной двухзвенной трещине скорость сходимости численных решений сингулярного интегрального уравнения ( ЗЛ06) и системы двух сингулярных интегральных уравнений (3.92) к точному почти одинакова. Поэтому нахождение численного решения с помощью уравнения (3.106) является более предпочтительным. [3]
Анализ численных результатов позволяет сделать следующие выводы. [4]
Анализ полученных многочисленных численных результатов для оболочек различного класса и различных параметров систем позволяет сделать некоторые общие выводы. Изменение параметров жесткости оболочек а, аь а2, 8 влияет на распределение контактного давления в меньшей степени, чем жесткости ложемента. С ростом жесткости ложемента давление существенно перераспределяется, возрастая на краях площадки контакта. Увеличение жесткости ложемента в ряде случаев приводит к появлению зон отрицательного давления, что может быть связано с отходом конструкции от ложемента. Данные вопросы более подробно рассмотрены в гл. [5]
Из анализа численных результатов следует, что траекторию уклонения на достаточно большом промежутке времени можно представить как ряд маневров, приводящих к последовательным сближениям и удалениям объекта Y от превосходящего его по скорости, но менее маневренного преследователя X. [6]
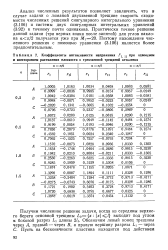
Переходим к анализу численных результатов. Рассмотрим, как влияет перемещение внешней поверхности на температурное поле внутри теплозащитного покрытия. [8]
Так как в настоящее время нет общего решения подобных задач, доказательство эффективности рассмотренных алгоритмов в основном сводится к анализу численных результатов достаточно большого числа расчетов на ЭЦВМ. [9]
 |
Зависимости приведенного пара -. ГГи-М метра о от г при ер 37 для низших гиб - ридиых WE g и Я. 21д - типов колебаний КДР при различных значениях у. [10] |
Аналогичные закономерности обнаружены и для гибридных типов колебаний КДР. Анализ численных результатов расчета показывает, что при равных условиях смещение резонансных частот гибридных НЕПб - и HE2i в - типов колебаний превышает смещение резонансной частоты основного Я01в - типа колебаний КДР. Вследствие этого проявляется важное свойство КДР - с ростом параметра у вырождение Я016 - и Я. [11]
Сравнение с точным ( быть может, гипотетически точным) решением. Последнее бывает известно в тестовых задачах, и часто его удается угадать в результате анализа численных результатов. [12]
Для случаев, когда L является дугой окружности ( точное решение ( 1.1 16)), гюлуэллипсом или дугой параболы. Было найдено также численное решение для трещины, размещенной вдоль дуги окружности. Анализ численных результатов показывает, что форма трещины сильно влияет на величину коэффициентов интенсивности напряжений. Для трещин, мало отличающихся от прямолинейной ( е 0 2), основное значение имеет ориентация концов трещины по отношению к основной ее части. [13]
Корректное моделирование движения пылевых частиц в такой плазме требует применения метода Броуновской динамики, который основан на решении системы обыкновенных дифференциальных уравнений с силой Ланжевена Гьг, учитывающей случайные толчки окружающих молекул газа: Для анализа динамики макрочастиц трехмерные уравнения движения решались при периодических граничных условиях. Анализ численных результатов показал, что нормированный параметр Г ( Ч к к2) ехр ( - к) Г полностью определяет корреляцию макрочастиц ( возникновение как дальнего, так и ближнего порядка в пылевой системе) и может рассматриваться как параметр, характеризующий упорядоченность частиц в системе Юкава от Г - 1 до точки ее кристаллизации, а динамика сильно-неидеальных систем Г 40 определяется двумя основными параметрами Г и с, последний из которых может рассматриваться как параметр масштабирования для диссипативных жидкостных систем. [14]
Страницы: 1