Оценка - математическое ожидание
Cтраница 2
При оценках математического ожидания и дисперсии случайного стационарного процесса следует выделить два граничных случая, зависящих от используемых экспериментальных данных. [16]
Найдем графически оценки математического ожидания и среднего квадратического отклонения предполагаемого нормального распределения. [17]
Как находятся оценки математического ожидания и дисперсии и каковы их свойства. [18]
Как вычисляется оценка математического ожидания методом, скользящего среднего. [19]
Найдем графически оценки математического ожидания и среднего квадратического отклонения предполагаемого нормального распределения. [20]
По точности оценки математического ожидания медиана уступает выборочному среднему. Однако при выборках небольшого объема предпочитают использовать Л, так как это облегчает вычисления. [21]
Для расчета оценок математического ожидания, дисперсии, среднеквадратичного отклонения, коэффициента асимметрии и эксцесса ( на основе моментов распределения) не требуется предварительного упорядочивания и группировки данных. Эти величины могут быть найдены непосредственно по исходной выборке. [22]
Что касается оценок математического ожидания, то очевидно, что для линейных систем расчетные формулы не отличаются от соответствующих соотношений для детерминированных сигналов, и мы не будем на них останавливаться, переходя сразу к оценкам вторых моментов. [23]
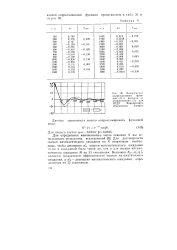 |
Эмпирическая корреляционная функция ( / и функция ее аппроксимации ( 2 для НГДУ Карадагнефть объединения Азнефть. [24] |
Для достоверности оценки математического ожидания по N скважинам необходимо, чтобы дисперсия з-т оценки математического ожидания т по N скважинам была такой же, как и для оценки математического ожидания М по 33 скважинам. Величина Кэ-От / ст. и является показателем эффективности оценки математического ожидания, а стм-дисперсия математического ожидания, определенная по 33 скважинам. [25]
Рассматривается задача оценки математических ожиданий аддитивных функционалов от траекторий диффузионных процессов, представляющих собой интегралы по некоторым областям расширенного фазового пространства от концентрации траекторий. Численное статистическое моделирование осуществляется по схеме Эйлера. Особенно трудоемкими для метода Монте-Карло являются указанные задачи в случае малых областей, когда фактически необходимо оценивать малые вероятности. [26]
Не практике для оценки математического ожидания испольвуют среднее арифметическое значение случайной величины. [27]
Ива нин В. М. Асимптотическая оценка математического ожидания числа элементов множества Парето. [28]
 |
Схема формирующего фильтра для моделирования случайной функции с экспоненциальной корреляционной функцией. [29] |
Рассмотрим задачу нахождения оценок математического ожидания и дисперсии случайной функции X ( t), являющейся стационарным эргодическим процессом. [30]
Страницы: 1 2 3 4