Задание - кривая
Cтраница 1
Задание кривой уравнениями ( 27, 1) называется параметрическим. [1]
Задание кривой у с помощью задания координат как функций параметра t называется параметрическим. [2]
Задание кривой уравнениями ( 27, 1) называется параметрическим. [3]
Такого рода задание кривой, когда одна из текущих координат ее точки представляется в виде ( однозначной) явной функции от другой координаты, мы будем называть явным заданием ( или представлением) кривой. Оно обладает простотой и наглядностью; как увидим, всякое другое задание - в некотором смысле - может быть сведено к этому. [4]
Такой способ задания кривой называется параметрическим, вспомогательная же переменная t - параметром. Для получения уравнения кривой в обычном ( явном или неявном) виде как зависимости, связывающей х и у, нужно из двух уравнений ( 9) исключить параметр t, что можно сделать, хотя бы решив одно из этих уравнений относительно t и подставив полученный результат в другое. [5]
Графическая или табличная форма задания кривой размагничивания не дает возможности в общем виде анализировать устройства с применением магнитнотвердых материалов. Поэтому часто пользуются приближенными аналитическими выражениями для кривой размагничивания магнитнотвердых материалов. [6]
Вектор-функции скалярного аргумента представляют собой удобный способ задания кривых в пространстве. [7]
В аналитической геометрии известны и другие способы задания кривых. [8]
 |
Понятие вектор-функции становится. [9] |
В дифференциальной геометрии вектор-функции одного аргумента используются для задания кривых. Для задания поверхностей пользуются вектор-функциями двух аргументов. [10]
В аналитической геометрии известны и ipyi ие способы задания кривых. [11]
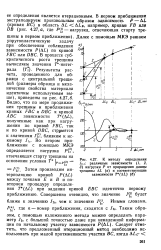 |
К методу определения 1 in с - различные зависимости ( 1, 2. [12] |
В и повторяем процедуру определения 7 ( AL) при задании кривой ЕВС идентично первому приближению. [13]
Очевидно, кривая определяется своим уравнением, поэтому можно говорить о задании кривой ее уравнением. [14]
Как будет показано далее, оба подхода можно применить при любом способе задания кривой. [15]
Страницы: 1 2 3