Задание - граничное условие
Cтраница 1
Задание граничных условий при принятой аппроксимации уравнений не вызывает затруднений. В граничных ячейках могут быть заданы давление или расход жидкости, в случае же непроницаемости границы гидропроводность в соответствующем направлении полагается равной нулю. [1]
Задание граничных условий в случае массообмена имеет ряд особенностей. Чтобы познакомиться с ними, рассмотрим процессы теплоотдачи и массоотдачи в двухкомпонентную среду или от нее. [2]
Задание граничных условий в случае массообмена имеет некоторые особенности. Чтобы познакомиться с ними, рассмотрим процессы теплоотдачи и массоотдачи в двухкомпонентную среду или от нее. [3]
Задание граничных условий: Дирихле, Неймана и смешанные. [4]
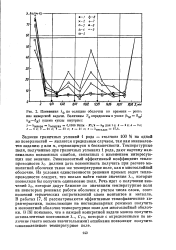 |
Изменения Яэ по толщине оболочки во времени - решение инверсной задачи. Величины Тд определены в узлах ( hM бм. Лкбк ( схема узлы внутри. [5] |
Задание граничных условий 1 рода - толчок 100 % на одной из поверхностей - является предельным случаем, так как эквивалентен заданию q или а, стремящемуся к бесконечности. Температурные поля, полученные при граничных условиях 1 рода, дают картину максимально возможных ошибок, связанных с изменением интересующих нас величин. Эквивалентный эффективный коэффициент теплопроводности Кэ должен дать возможность получить при расчете монолитной оболочки такое же температурное поле, как в многослойной оболочке. Из условия единственности решения прямых задач теплопроводности следует, что нельзя найти такие значения Я я, которые позволили бы получить одинаковые поля. Речь идет о получении значений А 9, которые дадут близкие по значениям температурные поля на некоторых режимах работы оболочек с учетом числа слоев, соотношений термических сопротивлений слоев контактов и металла. В работах [7, 8] рассматриваются эффективные теплофизические характеристики, позволяющие на нестационарных режимах получить в монолитной оболочке температурное поле для многослойной оболочки. В [8] показано, что в каждой конкретной задаче можно получить эквивалентные постоянные Кч, Суз, которые с определенными по величине ( часто весьма значительными) ошибками позволяют получить эквивалентное температурное поле. [6]
Задание граничных условий по tIT называется условием первого рода. Задание граничных условий по т называется условием второго рода. [7]
Рассмотрим задание граничных условий. Поскольку уравнения: (3.106) представляют уравнения равновесия узлов, то силовые граничные условия формируются автоматически. Из геометрических условий рассмотрим лишь простейший случай, когда запрещены в граничных узловых точках некоторые обобщенные перемещения в гло - f бальной системе координат. [8]
Такое задание граничных условий ( наложение связей можно рассматривать как расчет на заданные нулевые перемещения) имеет ряд существенных недостатков: расчет, на заданные перемещения труден с алгоритмической точки зрения; практически невозможно наложить связи ( и рассчитать на заданные перемещения) по направлениям, не совпадающим с направлениями осей выбранной системы координат; усилия в наложенных связях не вытекают из прямого расчета и их можно получить из рассмотрения условий равновесия соответствующего узла, что не очень удобно алгоритмически. [9]
Рассмотрим задание граничных условий. Поскольку уравнения: (3.106) представляют уравнения равновесия узлов, то силовые граничные условия формируются автоматически. Из геометрических условий рассмотрим лишь простейший случай, когда запрещены в граничных узловых точках некоторые обобщенные перемещения в гло - f бальной системе координат. [10]
Рассмотрим задание граничных условий. [11]
Для задания граничных условий служит специальная установка с подвижными водосливами, которая дает возможность представить на модели любой закон изменения уровней в трех различных вариантах. Таким образом, в общем случае одна установка граничных условий позволяет задать их в трех точках модели. [12]
Для задания граничных условий служит специальная установка с подвижным водосливом, которая позволяет задавать нестационарные граничные условия с любым законом изменения уровней в трех различных вариантах. В комплект гидроинтегратора входят установки с плавающими сосудами, которые служат для моделирования условий выделения скрытой теплоты при изменении агрегатного состояния среды. [13]
Такое задание граничных условий соответствует граничным условиям третьего рода. [14]
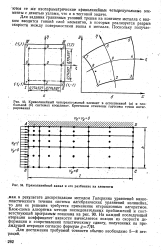 |
Криволинейный четырехугольный элемент в естественной ( а и глобальной ( о системах координат. Крестиком отмечены гауссовы точки интегрирования.| Прямолинейный канал и его разбиение на элементы. [15] |
Страницы: 1 2 3 4