Задача
Cтраница 1
Задачи, направляемые в компьютер и ждущие своей обработки в последовательности их поступления. [1]
Задача о влиянии парамагнетизма на спектры ЯМР нефтепродуктов является частным случаем интерпретации спектров ЯМР смесей диамагнитных и парамагнитных молекул. [2]
Задача состоит в определении энергий Ui и А причем последнюю надо найти как функцию температуры. Лишь в особо простых случаях это оказывается возможным приближенно. Беккером; обе фазы I и II должны иметь одинаковую решетку и очень близкие постоянные решетки. Энергия активации иг перехода молекулы из фазы I в фазу II может тогда быть принятой почти равной и - энергии активации для процесса обмена местами в решетке, которая определяется из температурной зависимости коэффициента диффузии. Труднее оказывается определение работы образования зародышей и соответственно необходимой для этого удельной свободной граничной энергии. Беккер принимает, что последняя равна энергии, которая необходима для образования поверхности раздела фаз в 1 см. При ее расчете, согласно Брэггу и Вильямсу [118], принимается, что атомы связаны только с ближайшими соседями. Энергия связи атома складывается из энергий связей с шестью соседями. [3]
Задача состоит в определении F с целью максимизации функции w из (2.122) при ограничениях по надежности конструкции. [4]
Задача о балке на упругом основании, простая и интересная с теоретической точки зрения, хорошо отражает основные характерные особенности более сложных задач проектирования при наличии контакта тел. Считается, что балка достаточно тонкая, поэтому для описания ее поведения ( зависимость деформации - сила) можно применить обыкновенную теорию балки. [5]
Задача, которая исследуется в данном разделе, отличается от рассмотренных выше своей направленностью на оптимальное проектирование. Поэтому проводится классификация параметров до того, как задача формулируется. [6]
Задача, определяемая соотношениями ( 3 68), (3.69), имеет вид параметрической оптимальной задачи разд. Поэтому она исследуется при помощи алгоритма параметрического оптимального проектирования. [7]
Задача сводится теперь к определению вариации ои ( х), обеспечивающей максимальное убывание я э0 при линеаризованных ограничениях. [8]
Задача о минимизации веса колонны уже рассматривалась в разд. Эта же задача решается ниже методом проекции градиента для иллюстрации применения данного метода к решению задач - оптимального проектирования. Используем математическую постановку задачи, приведенную ранее в разд. [9]
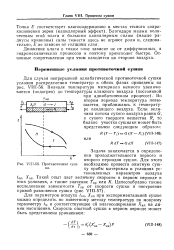 |
Противоточная сушка. [10] |
Задача заключается в определении продолжительности первого и второго периодов сушки. [11]
Задача 2.2. Пусть постоянная сосредоточенная сила Р при t 5э 0 приложена перпендикулярно к границе полуплоскости и движется с постоянной скоростью v вдоль оси х, при t 0 полуплоскость покоилась. [12]
Задача 3.4. Приведем решение задачи, аналогичной предыдущей, считая, что разрез распространяется под действием возрастающей во времени силы pt, сосредоточенной в начале координат. [13]
Задача 4.3. Рассмотрим динамическую задачу о расклинивании хрупкого тела. [14]
Задача сводится к управлению именно этими проектами. [15]
Страницы: 1 2 3 4