Данная вариационная задача

Cтраница 1

Данная вариационная задача решается в принципе так же, как это делалось в § 3.3, частные производные при этом заменяются вариационными производными. [1]

Бывает, что для данной вариационной задачи уравнения Эйлера - Лагранжа обращаются в нуль тождественно, и, значит, каждая функция является возможной экстремалью задачи. [2]

Точная степень гладкости, требующаяся для экстремалей данной вариационной задачи, пространство функций, на котором нужно искать экстремали, и подходящая норма ( или нормы) - это, вообще говоря, довольно деликатные вопросы, требующие развитого нелинейного функционального анализа. Сложные проблемы, возникающие здесь, не имеют, однако, прямого отношения к нашей непосредственной области исследования. Поэтому для упрощения мы рассматриваем лишь гладкие ( С00) экстремали вариационной задачи. Распространение наших результатов на группы симметрии и законы сохранения для более общих типов функций должно учитывать специфику конкретной задачи. [3]

Оно является условием стационарности функционала (1.1) и называется уравнением Эйлера данной вариационной задачи. [4]

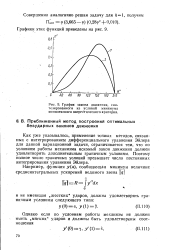График закона движения, синтезированного из условий минимума комплексного энергетического критерия. [5]

Как уже указывалось, применение точных методов, связанных с интегрированием дифференциального уравнения Эйлера для данной вариационной задачи, ограничивается тем, что по условиям работы механизма искомый закон движения должен удовлетворять дополнительным граничным условиям. Поэтому полное число граничных условий превышает число постоянных интегрирования уравнения Эйлера. [6]

Понятие о допустимости выбора некоторой последовательности функций вида ( 176) в качестве координатных функций данной вариационной задачи обычно включает требования удовлетворения этими функциями определенным краевым условиям, линейной независимости функций на некотором интервале, а также определенным свойствам гладкости. [7]

Функции у ( х) или yi ( х), удовлетворяющие уравнению или уравнениям Эйлера для данной вариационной задачи, называются экстремалями рассматриваемой задачи; они образуют 2 / г-параметрическое семейство. [8]

Функции у ( х) или У ( ( х), удовлетворяющие уравнению или уравнениям Эйлера для данной вариационной задачи, называются экстремалями рассматриваемой задачи; они образуют 2 / г-параметрическое семейство. [9]

Якоби указал на то, что эта форма неудовлетворительна, потому что время t не может рассматриваться как аргумент в данной вариационной задаче. Действительно, наш процесс уменьшения числа степеней свободы еще не закончен. Мы должны исключить циклическую переменную / при помощи уравнения для импульса (5.6.3), а это делает / зависимой переменной. [10]

Уже в статьях, посвященных обобщенным кривым ( 1933 - 1938 гг.), Янг предложил совершенно новый для того времени подход, а именно возможность рассматривать кривую или поверхность как функционал в пространстве подинтеграль-ных выражений, отвечающих данной вариационной задаче. [11]

Непосредственный подбор приближенных выражений для плотности вероятности должен сопровождаться выполнением ряда требований. Аппроксимирующие функции должны удовлетворять дополнительным условиям в форме моментных соотношений, обладать свойствами полноты, дифференцируемое, непрерывности. Свойство ортогональности базисных функций, которое обычно используют при построении приближенных решений, в данной вариационной задаче теряет свое значение. Более важны такие требования, как неотрицательность функции р ( и), ее затухающий характер при и, стремящемся к бесконечности, а также практическая сходимость процесса построения приближенного решения. [12]

Приведенный там метод нахождения мультиплетов основан на распределении между атомами спинов электронов всеми возможными способами. Каждому распределению ставится в соответствие детерминантная функция. Далее ищется результат действия на эти де-терминантные функции всех операций точечной группы. Найденные таким способом представления отвечают определенным значениям проекции полного спина Ms. Представления, отвечающие определенным значениям полного спина S, находятся вычитанием друг из друга представлений с разными Ms. Подобный метод достаточно громоздок уже для сравнительно простой задачи нахождения 14 мультиплетов, возникающих от ковалент-ных структур ( см. [38], стр. Метод, изложенный в предыдущем разделе, позволяет без особого труда найти все 268 мультиплетов, возникающих в данной вариационной задаче. Рассмотрим процесс нахождения этих мультиплетов последовательно. [13]

Страницы: 1