Случай - движение
Cтраница 3
Некоторые случаи движения твердого тела - в частности, движение физического маятника - рассматривались еще до Ньютона, Галилей обнаружил изохронность колебаний маятника. Триста пятьдесят лет тому назад Галилей в кафедральном соборе, видимо, с гораздо большим вниманием следил за качанием паникадила, нежели слушал мессу и проповедь архиерея. Паникадило, висевшее из высокого купола собора, совершало размахи, примерно в 7 секунд, справа налево, так что Галилею было легко вести двойной счет размахов и биения своего пульса. Месса была длинная; размахи паникадила становились все меньше и меньше, а между тем продолжительность каждого размаха оставалась неизменной. [31]
Лагранжев случай движения весомого твердого тела вокруг неподвижной точки. Пусть весомое твердое тело S движется вокруг неподвижного полюса О, для которого эллипсоид инерции тела является поверхностью вращения. Этот случай движения тела носит название лагранжева случай движения весомого твердого тела, а само тело называется симметричным весомым гироскопом. [32]
Лагранжев случай движения весомого твердого тела вокруг неподвижной точки. Пусть весомое твердое тело S движется вокруг неподвижного полюса О, для которого эллипсоид инерции тела является поверхностью вращения. Этот случай движения тела носит название лагранжева случая движения весомого твердого тела, а само тело называется симметричным весомым гироскопом. [33]
Для случая движения в трубе интересные результаты о поле турбулентных пульсаций получены Лауфером [134] при помощи термоанемометра. [34]
Оба случая движения существенно отличаются друг от друга и обуславливают необходимость применения различных расчетных формул. [35]
Для случая движения точки по плоскости секторная скорость перпендикулярна этой плоскости, если точка О выбрана в той же плоскости, в которой движется точка. Секторная скорость всегда приложена в той точке, относительно которой она вычисляется. [36]
Для случая движения точки по плоскости секгорная скорость перпендикулярна этой плоскости, если точка О выбрана в той же плоскости, в которой движется точка. Секторная скорость всегда приложена в гой точке, относительно которой она вычисляется. [37]
Оба случая движения газа существенно отличаются и обусловливают применение различных расчетных формул. [38]
Для случая движения раствора под воздействием перемещающейся колонны труб в работе [35] рекомендуется пользоваться выражением обобщенного критерия Рейнольдса для кольцевого-пространства. [39]
Для случаев движения жидкости или газа внутри труб некруглого сечения коэффициент трения определяется по тем же формулам, что и для круглых труб, но в качестве линейного размера при подсчете числа Re принимается эквивалентный диаметр. [40]
Для случая движения потоков в трубопроводах или аппаратах любых размеров обычно в качестве определяющего линейного размера берется диаметр трубы круглого сечения или эквивалентный диаметр некруглого сечения. [41]
Для случая движения жидкости в пористой среде эти классические уравнения практически не применяются из-за невозможности описать граничные условия. [42]
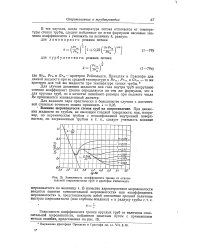 |
Зависимость коэффициента трения от относительной шероховатости труб и критерия Рейнольдса. [43] |
Для случаев движения жидкости или газа внутри труб некруглого сечения коэффициент трения определяется по тем же формулам, что и для круглых труб, но в качестве линейного размера при подсчете числа Re принимается эквивалентный диаметр. [44]
Для случая движения точки по плоскости секторная скорость перпендикулярна к этой плоскости, если точка О выбрана в той же плоскости, в которой движется точка. Секторная скорость всегда приложена в той точке, относительно которой она вычисляется. [45]
Страницы: 1 2 3 4