6-угольник
Cтраница 1
Дважды пройденные 6-угольники классов АСО-6-параллелограммов, призм и аффинно-правильных 6-угольников образуют еще четыре циклических класса, отличных от вышеуказанных. [1]
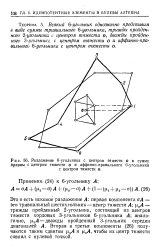 |
Разложение б-угольника с центром тяжести о в сумму. [2] |
Всякий 6-угольник однозначно представим в виде суммы тривиального 6-угольника, трижды пройденного 2: угольника с центром тяжести о, дважды пройденного 3-угольникс. [3]
Для всякого 6-угольника А шестиугольник А является призмой. [4]
Типичный атомарный класс 6-угольников состоит из аффинно-правильных 6-угольни-ков с центром тяжести о. Для произвольного п типичные атомарные классы описаны в гл. [5]
Вместе с классом тривиальных 6-угольников эти классы образуют полный набор атомарных циклических классов. [6]
Если А - некоторый 6-угольник, то А не обязан быть 6-параллелограммом. Можно, однако, поставить вопрос о том, нельзя ли указать отображение, которое переводит множество всех 6-угольников в класс 6-параллелограммов. [7]
Например, если / CQ, то 6-угольники, у которых отсутствует аффинно-правильная компонента, являются призмами ( см. § 5 гл. [8]
Тогда призму можно будет определить как такой 6-угольник, для которого в V существует параллельный перенос, переводящий точки первой строки таблицы в соответствующие точки второй строки. [9]
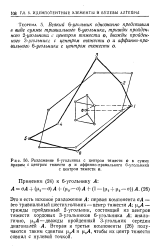 |
Разложение б-угольника с центром тяжести о в сумму. [10] |
Всякий 6-угольник однозначно представим в виде суммы тривиального 6-угольника, трижды пройденного 2: угольника с центром тяжести о, дважды пройденного 3-угольникс. [11]
Итак, Q-правильными являются 12-угольники, оба хордовых 6-угольника которых аффинно-пра-вильны и изобарпчны. [12]
Диаграмма классов 8-угольников отличается от диаграммы восьми классов 6-угольников: периодические классы образуют в ней цепочку, призмы и аффинно-пра-вильные 8-угольники отсутствуют. Классы дважды пройденных 4-угольников образуют поддиаграмму нашей диаграммы, совпадающую с диаграммой 4-уголышков. [13]
Легко указать восемь циклических классов, аналогичных классам 6-угольников. [14]
Дважды пройденные 6-угольники классов АСО-6-параллелограммов, призм и аффинно-правильных 6-угольников образуют еще четыре циклических класса, отличных от вышеуказанных. [15]
Страницы: 1 2