Adi-метод
Cтраница 1
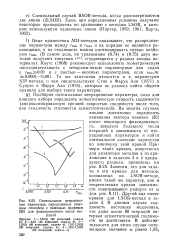 |
Оптимальные итерацион - о г янном ГГТУЧЯР г п. [1] |
Опыт применения ADI-методов показывает, что распределение параметров между rmm и гтах и их поряДок не являются решающими, и их сходимость можно оптимизировать только подбором гшщ. Те же замечания относятся и к параметрам SIP-метода, о чем свидетельствуют Стин и Фарук Али ( 1971) и Суарес и Фарук Али ( 1976), которым не удалось найти общего правила для выбора таких параметров. [2]
Для вывода уравнений ADI-метода Дуглас использовал аппроксимацию Кранка - Николсона. [3]
Существует много других вариантов ADI-методов, но здесь их рассматривать не будем. Интересующиеся должны обратиться к упомянутым1 ранее источникам. [4]
Шеффилд сравнил данный метод с методом Саульева ( попеременное использование уравнений (7.86) и (7.87) и с ADI-методом. ADI-метод оказался точнее в сравнении с методом Саульева по линиям для задачи с квадратной сеткой, но метод Саульева по линиям был значительно точнее для задачи с вытянутой сеткой. Поточечный метод Саульева был наименее точен в обоих случаях. Это характерно для ADI-методов. Подобные недостатки присущи и итерационным ADI-методам, плохо сходящимся для таких задач ( см. гл. [5]
Шеффилд сравнил данный метод с методом Саульева ( попеременное использование уравнений (7.86) и (7.87) и с ADI-методом. ADI-метод оказался точнее в сравнении с методом Саульева по линиям для задачи с квадратной сеткой, но метод Саульева по линиям был значительно точнее для задачи с вытянутой сеткой. Поточечный метод Саульева был наименее точен в обоих случаях. Это характерно для ADI-методов. Подобные недостатки присущи и итерационным ADI-методам, плохо сходящимся для таких задач ( см. гл. [6]
Авторы показывают, что с помощью ADE-метода при блочно-центрированной сетке не удается на внешних границах выполнить условия отсутствия течения флюида через них, что приводит к погрешностям в материальном балансе. Коутс и Терхьюн также установили, что ADI-метод значительно точнее ADE-метода, а вычислений для первого требуется лишь на 60 % больше. [7]
Рассматриваемые здесь ADI-методы иногда называются безытерационными в отличие от тех ADI-методов, в которых для решения матричных уравнений используются итерации ( см. гл. [8]
Они обнаружили, что при больших временных шагах возникают осцилляции. Это характерно и для метода Кранка - Николсона ( CN), поскольку ADI-метод - разновидность CN-метода. [9]
Шеффилд сравнил данный метод с методом Саульева ( попеременное использование уравнений (7.86) и (7.87) и с ADI-методом. ADI-метод оказался точнее в сравнении с методом Саульева по линиям для задачи с квадратной сеткой, но метод Саульева по линиям был значительно точнее для задачи с вытянутой сеткой. Поточечный метод Саульева был наименее точен в обоих случаях. Это характерно для ADI-методов. Подобные недостатки присущи и итерационным ADI-методам, плохо сходящимся для таких задач ( см. гл. [10]
Затем изменим направление упорядочения неизвестных и с помощью уравнения ( 8.73 а) найдем u ( v 1), рассматривая неизвестные вдоль каждой линии в направлении оси у. Процесс продолжается до достижения сходимости результатов. Возможности указанных методов могут быть реализованы только при использовании в цикле последовательно параметров r ( m) и повторении циклов до тех пор, пока ы ( у) не сойдется с и. В этом заключается основная проблема, возникающая при использовании ADI-методов, - установить, каково оптимальное число итераций в цикле и каковы оптимальные параметры для цикла. [11]
Для связанных уравнений выбор аппроксимации по времени имеет решающее значение. Поскольку уравнение ( 5.1 а) параболическое, то представляются естественными попытки использования методов, изложенных в гл. Однако при решении систем нелинейных связанных уравнений данного типа по этим методам редко получают положительный результат. Как указывал Писман ( 1967), явный метод, как и неявный метод переменных направлений Писмана - Рэчфорда ( ADI-метод), для задач данного типа неустойчив. Более надежен метод с аппроксимацией уравнений обратной разностью. Дуглас ( 1960) показал, что по этому методу получают устойчивые решения задач двухфазной фильтрации. Данный метод наиболее часто используется при моделировании нефтяных пластов. [12]
Страницы: 1