Расширенные bst-деревья
Cтраница 1
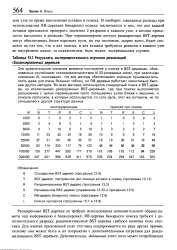 |
Результаты экспериментального изучения реализаций. [1] |
Расширенные BST-деревья не требуют использования дополнительного объема памяти под информацию о балансировке; RB-деревья бинарного поиска требуют 1 дополнительного разряда; рандомизованные BST-деревья требуют наличия поля счетчика. Для многих приложений поле счетчика поддерживается по ряду других причин, поэтому оно может быть и не сопряжено с дополнительными затратами для рандо-мизованных BST-деревьев. [2]
Сравните расширенные BST-деревья со стандартными BST-деревьями применительно к задаче построения индекса из фрагмента реального текста, содержащего по меньшей мере 1 миллион символов. Измерьте время, требуемое для построения индекса и средние длины путей в BST-деревьях. [3]
Подводя итоги, можно сказать, что все рассмотренные в этой главе методы обеспечат высокую производительность для типовых приложений, при этом каждый метод обладает собственными достоинствами для тех, кто заинтересован в разработке высокопроизводительных реализаций таблиц символов. Расширенные BST-деревья обеспечат высокую производительность как метод самоорганизующегося поиска, особенно, когда частое обращении к небольшим наборам ключей является типичным случаем; рандомизованные BST-деревья, вероятно, будут работать быстрее и их проще реализовать для таблиц символов, которые должны обладать полным набором функций. Списки пропусков просты для понимания и могут обеспечить логарифмическую зависимость времени поиска при меньших затратах памяти, а RB-деревья бинарного поиска привлекательны для библиотечных реализаций таблиц символов, поскольку они обеспечивают гарантированные предельные характеристики производительности для худшего случая и являются наиболее быстрыми алгоритмами поиска и вставки случайных данных. [4]
Не следует выполнять какие-либо поиски: просто постройте деревья и вычислите длину их путей. Являются ли расширенные BST-деревья сбалансированными в большей степени, чем произвольные BST-деревья, в меньшей степени или так же. [5]
 |
Результаты экспериментального изучения реализаций. [6] |
И наоборот, накладные расходы при использовании RB-деревьев бинарного поиска заключаются в том, что для каждой вставки приходится проверять значение 2 разрядов в каждом узле, а иногда приходится выполнять и ротацию. При неравномерном доступе расширенные BST-деревья могут обеспечивать более короткие пути, но эта экономия, скорее всего, будет сводится на нет тем, что и для поиска, и для вставки требуются ротации в каждом узле во внутреннем цикле, за исключением, быть может, экстремальных случаев. [7]
Страницы: 1