Алгоритм - метод
Cтраница 1
Алгоритм метода заключается в отыскании осевого направления, вдоль которого функция цели уменьшается наиболее сильно. Для этого в начальной точке поиска определяются производные оптимизируемой функции по всем независимым переменным. [1]
Алгоритм метода сравнительно не сложен. [2]
Алгоритм метода строится следующим образом. [3]
Алгоритмы метода Монте-Карло для решения интегральных уравнений можно улучшать, используя априорную информацию о решении - сопряженного уравнения. [4]
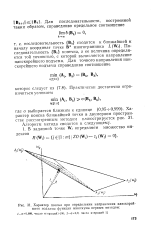 |
Характер поиска при определении направления наискорейшего подъема функции минимума первым методом. / - 0 - 0 999, число тераццй100. 2 - а0 9, число итераций 12. [5] |
Алгоритм метода сводится к следующему. [6]
 |
Четыре типа форм оболочки. [7] |
Алгоритм метода в значительной степени зависит и от способа постановки граничных условий на поверхности контакта оболочки с газом. Непосредственное применение способов, используемых для объемных тел и заключающихся во введении в тело слоя фиктивных ячеек, в данном случае затруднено из-за того, что тонкая оболочка моделируется поверхностью, не имеющей толщины. Для того, чтобы можно было проводить расчеты как для внутренних, так и граничных ячеек на основе единого алгоритма, в вычислительной сетке оболочка моделируется в виде совокупности вырожденных ячеек нулевой толщины. Расчеты показали, что такая неравномерность площадей вносит заметную погрешность. Эта погрешность является следствием ошибки, допускаемой при вычислении массы в узле, прилегающем к треугольной ячейке. [8]
Алгоритм метода характеристик не требует для моделирования миграции решения системы уравнений. [9]
Алгоритм метода деформаций рационально использовать только как одну из возможностей расширения границ приложения метода сил. [10]
Алгоритм метода конфигураций состоит из следующих операций. Прежде всего задается начальная точка Х, а также начальное приращение ДХ. Чтобы начать пробные шаги, следует вычислить значение функции F ( X) в начальной точке. Затем в циклическом порядке изменяется каждая переменная ( каждый раз только одна) на выбранные значения приращений, пока все параметры не будут таким образом изменены. [11]
Алгоритмы метода ветвей и границ различаются стратегией ветвления и принципами оценивания. Стратегии ветвления определяются обычно нижними оценками, построенными на последнем шаге и, возможно, на предыдущих шагах. Усиление оценок позволяет ускорить вычислительный процесс. При решении практических задач стратегии ветвления и оценивания определяются обычно эвристическими соображениями, существенно использующими специфику задачи. [12]
Алгоритм метода проверки основан на интегрировании уравнения (4.42) при Р const ( изобарические данные) во всех прилежащих парах экспериментальных значений концентрации компонента в жидкой фазе, записанном для бинарной смеси. [13]
Алгоритмы метода прогонки в отличие от более общих алгоритмов учета разреженности матриц с нерегулярной структурой характеризуются большей простотой программной реализации. [14]
Алгоритм метода приращений чрезвычайно прост. Выполняется ( tt 1) вариант анализа работы схемы. В первом варианте задаются номинальные значения всех управляемых параметров. В результате будет получен вектор номинальных значений выходных параметров УНОМ. В следующем варианте задается некоторое отклонение AW1W1 - WHOM 1 от номинального значения только первому из управляемых параметров. [15]
Страницы: 1 2 3 4