Алгоритм - даюта
Cтраница 1
Алгоритмы дают весьма компактные решения и пригодны для вложения в ОВС автоматов с несколькими десятками букв в МДНФ, реализуемой переключательной функции. [1]
Эти алгоритмы дают неплохие результаты в медицинской томографии, где число направлений наблюдений обычно весьма велико. Однако в задачах плазменной томографии для малого числа ракурсов особое значение приобретают итерационные методы, позволяющие получать приближенные оценки томограмм путем последовательного введения в алгоритм априорной физической информации. [2]
Представление об эффективности этого алгоритма дают графики рисунка, построенные для случая т 100, ттах 1, щ 1, а 0 1, bik - 0 15, в котором величины TJ полагались случайными с равномерным законом распределения в интервале [ ai: ттах ], значения их выбирались из таблицы случайных чисел. [3]
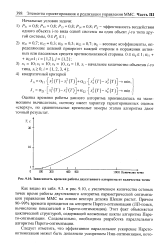 |
Зависимость времени работы двухэтапного алгоритма от количества точек. [4] |
Оценка времени работы данного алгоритма производилась на маломощном вычислителе, поэтому имеет характер гарантированных оценок сверху, но сравнительные временные замеры этапов алгоритма дают точный результат. [5]
Для наихудших элементов /, т.е. таких /, что Ц Sf - ф ( 9 ( /)) е ( ф), оптимальные по точности алгоритмы дают наилучшую возможную аппроксимацию. Для пользователя, который, может быть, хочет решить задачу как раз для такого легкого /, это весьма нежелательное свойство. Поэтому в настоящей главе мы изучим алгоритмы, которые не только оптимальны ( или близки к оптимальным), но и таковы, что для каждого f из 9 локальная погрешность почти минимальна. [6]
Существенным дополнением к тем постановкам и результатам, которые содержатся в данном пособии, могут служить ряд следующих оригинальных достижений в [785]: 1) показано, что для класса линейных задач и линейной исходной информации оптимальные пассивные и последовательные ( адаптивные) алгоритмы дают один и тот же результат; 2) исходная информация в виде конечного набора функционалов представлена одним нелинейным функционалом; 3) показано также, что для нелинейных задач адаптивная линейная информация может иметь существенное преимущество перед пассивной; 4) для ряда задач указаны нижние грани ошибок оптимальных алгоритмов по всем способам задания допустимой информации; 5) определены связи между основными понятиями теории оптимальных алгоритмов и экстремальными задачами теории аппроксимации; 6) построена иерархия сложностей решения задач и показано существование задач с произвольной сложностью; 7) исследованы максимальные скорости сходимости и сложности итеративных процессов при данной информации. [7]
Отн алгоритмы дают возможность машине на основе просмотра нескольких примеров изображений, подлежащих анализу, самостоятельно строить язык их описания. Такой язык в свою очередь может далее быть использован как основа программного обеспечения диалога человека и машины с помощью картинок. [8]
Алгоритмы предусматривают последовательно-параллельный принцип выполнения проекта, а также внесение изменений в проектирование с помощью корректирующих обратных связей. Это позволяет применить итерационный поиск рациональных проектных решений, координируемый во времени по этапам проектирования. Таким образом, алгоритмы дают возможность правильно распределить работы на этапах выполнения технического задания, технического и рабочего проектов, внедрения системы. [9]
Пересчитать все города в стране с населением более одного миллиона - это значит назвать цифру, а перечислить такие города - это огласить список городов. Алгоритмы комбинаторики легко позволяют решить задачи перечисления элементов множества. Некоторые из задач перечисления решаются без ЭВМ с помощью производящей функции ( энумератора) [4], но далеко не все. Кроме того, использование производящей функции занимает гораздо больше времени, чем составление алгоритмов, написание и отладка программ. При необходимости и задачи пересчета могут быть решены с помощью алгоритмов комбинаторики, хотя большинство задач пересчета решается без ЭВМ. Надо только не забывать, что алгоритмы дают ответ в числах для каждого конкретного примера пересчета, а теория дает ответ в формулах, объединяющих группу примеров пересчета. [10]
В модели строится последовательность преобразований матриц, отвечающая требованиям группы задач трудового нормирования. В результате рассмотрения зависимостей между построенными матрицами выделяется достаточный для реализации всех задач Eia-бор матричных операций. В модели, отвечающей процессу трудового нормирования на московском заводе Красный пролетарий, выделяются операции умножения матрицы на число, сложения столбцов матрицы, сложения подмножеств строк матрицы, сложения матриц. Списковая организация массивов данных позволяет запоминать только ненулевые элементы рассматриваемых в модели матриц. В то же время списковая организация массивов позволяет нам: производить быстрый поиск самих матриц, число которых велико, а также эффективно вносить изменения в них, связанные как с появлением новых ненулевых элементов, так с исключением и заменой старых. При этом используются стандартные процедуры поиска и внесения изменений. Далее устанавливается однозначное соответствие между списковой формой записи данных в памяти ЭЦВМ и записью ненулевых элементов матрицы. Установленное соответствие позволяет свести операции над матрицами к операциям над списками. Затем строятся алгоритмы выполнения указанных матричных операций над списками, организованными последовательным способом. Алгоритмы сложения матриц и сложения подмножеств строк основаны на использовании минимального дерева, описанного в [5], в качестве диаграммы стратегии объединения отсортированных групп данных по двум путям. Поэтому эти алгоритмы дают минимально возможное при объединении число операций сравнения, максимально используя порядок, уже имеющийся в данных. Программирование всех задач в подсистеме трудового нормирования организуется с помощью компилирующей системы поисковых процедур и матричных операций над элементами списков. Особенно эффективна для реализации указанной компилирующей системы мультипрограммная ЭЦВМ, дающая возможность задавать приоритет задач и организовывать прерывание их для решения задач с большим приоритетом. [11]
Страницы: 1