Модифицированный алгоритм
Cтраница 1
Модифицированный алгоритм в конечном счете встречает только записанные ранее тройки и завершает свое действие. Последние две строки табл. 5.2.2 служат иллюстрацией нового затруднения. Эта проблема возникла в результате того, что в правой части правила Т: : - TIP содержались два нетерминальных символа, а предыдущее расширение СПНС не подразумевало расширения символов слева от него. В данном конкретном случае1 эту проблему можно устранить, рассматривая нетерминал ( нетерминальный символ) в ранее записанном контексте как квазитерминал и используя следующий нетерминал как новый СПНС. Однако в общем случае расширение истинного СПНС дает символы, которые должны стать правым контекстом для нового СПНС. Может показаться, что мы попали из огня да в полымя. Расширяя символ только один раз в каждом контексте, мы гарантируем, что алгоритм завершится, но он не может породить все действительные контексты. [1]
Модифицированный алгоритм позволяет не только отражать, но и сжимать и расширять треугольник. [3]
Модифицированный алгоритм Осборна [61 ] для матрицы Z работает следующим образом. Однако преобразование подобия нужно проводить для всей матрицы. [4]
Модифицированный алгоритм Басакера - Гоуэна. [5]
Модифицированный алгоритм Басакера - Гоуэна в задаче о потоках с множителями может не обеспечивать сходимости. Рассмотрим прием, гарантирующий достаточную для практики точность и быстродействие. Будем считать, что поток хц насыщает дугу и графа приращений, если 7 - х ц е, где е - число, определяющее точность вычислений. [6]
Модифицированный алгоритм отсечения усложнен за счет анализа случая пересечения прямых с плоскостью - Ze 0, рассмотренного в разд. [7]
Модифицированные алгоритмы имитации отжига используются также для решения задач комбинаторной оптимизации. [8]
Модифицированный алгоритм линейного решета был запрограммирован автором на языке Си. Для апробации алгоритма были выбраны простые модули логарифмирования 16628713074077671199, 73241790487976404907266296887, 319265159717924402858789797769075519279, р ( 49) 1296753200212444961524194658808160151815781927547, р ( во) 314159265358979323846264338327950288419716939937510582145843, содержащее 20, 29, 39, 49 и 60 десятичных знаков, соответственно. [9]
 |
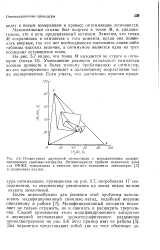
Результаты оптимизационных расчетов. [10] |
Модифицированный алгоритм последовательных уступок характеризуется более детальным и целенаправленным исследованием совместного поведения частных функций цели в выбранной области пространства параметров оптимизации и, следовательно, может давать более точные результаты. Однако последний алгоритм оказывается и более сложным в реализации. [11]
Такой модифицированный алгоритм формирует управляющее воздействие на основе компромисса между хорошим управлением и хорошим оцениванием. Несмотря на кажущуюся простоту алгоритма управляющее воздействие определяется лишь численно. Недостатком метода является определенный произвол в выборе коэффициентов при добавке к основному функционалу, зависящей от ошибки оценивания. [12]
Выполните модифицированный алгоритм, предложенный в упражнении 8.18, для крупных файлов с произвольной организацией. [13]
ВыЕкхпните модифицированный алгоритм, предложенный и упражнении 8.1 Я, для крупных файлов с и ро и j РОЛЬНОЙ организацией. [14]
Рассмотрите модифицированный алгоритм SYNTHESIZE из разд. [15]
Страницы: 1 2 3 4