Двухэтапный алгоритм

Cтраница 1

Двухэтапные алгоритмы нередко используются при решении задач коррекции по данным геофизических полей. Таким образом, для решения существенно разных по смыслу задач используются одни и те же пути построения упрощенных алгоритмов, основанные на использовании аппарата теории нелинейной фильтрации. [1]

Двухэтапные алгоритмы нередко используются при решении задач коррекции по данным геофизических полей. [2]

Так, в монографии [195] сформирован двухэтапный алгоритм получения аналога Нэш-равновесного управления на основе достаточных условий абсолютного максимума Кротова, если существуют и могут быть определены специальные функции. В [329] дано необходимое условие программного равновесия на основе функции Гамильтона с методом двусторонней прогонки при решении краевой задачи - пинг-понг алгоритмом. В [334] сформированы достаточные условия получения Нэш-программных управлений на основе условия экстремума гамильтониана j - ro игрока ( г Г - N) при условии линейности гамильтониана по состоянию и разделимости по управлению и состоянию. В [349] получено достаточное условие равновесных стратегий на основе функции Гамильтона, причем данное условие удобно для верификации управлений, полученных из необходимых условий. [3]

На рис. 5.2 дана структурная схема двухэтапного алгоритма Шепли-оптимизации ММС. [4]

Идея пропорционального распределения была реализована в виде двухэтапного алгоритма расчетов, предложенного И.И.Дикиным [36], в котором существенно используется свойство метода внутренних точек вырабатывать относительно внутреннюю точку множества оптимальных решений задачи линейного программирования. Это свойство означает, что граничные значения по условиям-неравенствам (2.3.2) - (2.3.4) достигаются только для тех переменных, которые имеют эти граничные значения при любом другом оптимальном решении. [5]

Когда значения k и п велики, величина погрешности для двухэтапного алгоритма может стать недопустимо большой. [6]

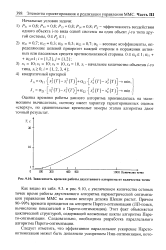Зависимость времени работы двухэтапного алгоритма от количества точек. [7]

Как видно из табл. 9.3. и рис. 9.10, с увеличением количества сетевых точек время работы двухэтапного алгоритма параметрической оптимизации управления ММС на основе вектора дележа Шепли растет. Этот факт объясняется циклической структурой, содержащей вложенные циклы алгоритма Парето-оптимизации. Следовательно, необходима разработка параллельного алгоритма Парето-оптимизации. [8]

Из выражения для Л 1 следует, что ее коэффициенты зависят от неизвестной функции Fit), производная от которой и есть искомая плотность вероятности. Поэтому предлагается следующий двухэтапный алгоритм восстановления плотности. [9]

Сложные многокритериальные задачи ( с их проблемой глобальной оптимизации) поиска стабильных и эффективных решений и их комбинаций на достаточно сложных прикладных моделях требуют изучения более гибких методов, алгоритмов и процедур оптимизации управления ММС. Поэтому актуально применение двухэтапных алгоритмов оптимизации с сетевым поиском начальных приближений и точным решением в локальной области. [10]

Для данного счетного шага по времени сначала решается газодинамическая часть системы, которая получается, если все турбулентные члены в уравнениях ( jw, rw, qw ] положить равными нулю. Расчет газодинамических параметров проводится по двухэтапному алгоритму. Первый этап - лагранжев, второй - этап перестройки сетки и конвективного переноса. На лагранжевом этапе учитывается только действие сил давления и вычисляются промежуточные значения скорости и, внутренней энергии е и координат узлов z, плотность считается неизменной. [11]

Страницы: 1