Непрямой алгоритм - оптимизация
Cтраница 1
Непрямые алгоритмы оптимизации отличаются следующими особенностями: используя глобальную информацию относительно поведения целевой функции -, они становятся малочувствительными к локальным экстремумам; алгоритмы являются поисковыми, т.е. для них не требуется производить вычисления градиентов; для работоспособности и в определенной степени эффективности алгоритмов не требуется точная аппроксимация функции ( точность модели), особенно в начале поиска; если пользователь уже проделал определенное количество экспериментов с моделью, то результаты экспериментов применяются алгоритмами в начале поиска, т.е. используются активно-пассивные методы обработки данных. [1]
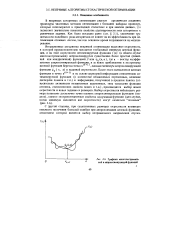 |
Графики многоэкстремальной и аппроксимирующей функций. [2] |
В непрямых алгоритмах оптимизации удается органически соединить процедуры численных методов оптимизации с большим набором процедур, которые используются в прикладной статистике и при анализе данных, что позволяет значительно повысить свойства адаптируемости этих алгоритмов к различным задачам. Как было показано ранее ( см. § 3.1), увеличение трудоемкости подобного рода алгоритмов не влияет на их эффективность при оптимизации сложных систем, так как основное время затрачивается на моделирование. [3]
Далее будут приведены базовые непрямые алгоритмы оптимизации и их модификации в зависимости от модели аппроксимирующей функции. [4]
Простой, но достаточно эффективный непрямой алгоритм оптимизации со структурно-параметрической адаптацией состоит в следующем: в зависимости от размеров плана эксперимента на k - к итерации и количества проделанных ранее экспериментов включается в работу один из описанных базовых непрямых алгоритмов оптимизации. [5]
Опишем один из непрямых алгоритмов оптимизации - с базовой неполной квадратичной моделью, являющийся адаптивным к выбору компонентов вектора независимых переменных. Идея его заключается в выделении на каждой итерации группы независимых переменных, оказывающих наибольшее влияние на изменение целевой функции. [6]
Отметим важное достоинство непрямых алгоритмов оптимизации - движение к экстремуму осуществляется после каждого нового вычисления целевой функции. [7]
В настоящее время известен ряд непрямых алгоритмов оптимизации на основе МГУА, в том числе поэтапный, где изложенную выше последовательность шагов следует рассматривать как одну итерацию поиска экстремума оптимизируемой функции. [8]
Таким образом, пользователь при конструировании непрямых алгоритмов оптимизации может учесть фактически любые априорные сведения о решаемой задаче. [9]
Все алгоритмы однопараметрической стохастической оптимизации, описанные в § 3.2 и использующиеся в непрямых алгоритмах оптимизации, по своему замыслу могут быть также отнесены к непрямым алгоритмам оптимизации. [10]
Проблема выбора шагового множителя pv и генерации плана эксперимента Х решается так же, как в квазиградиентном непрямом алгоритме оптимизации. В качестве критерия останова используется тот же критерий, что и в квазиградиентном непрямом алгоритме оптимизации. [11]
Все алгоритмы однопараметрической стохастической оптимизации, описанные в § 3.2 и использующиеся в непрямых алгоритмах оптимизации, по своему замыслу могут быть также отнесены к непрямым алгоритмам оптимизации. [12]
Простой, но достаточно эффективный непрямой алгоритм оптимизации со структурно-параметрической адаптацией состоит в следующем: в зависимости от размеров плана эксперимента на k - к итерации и количества проделанных ранее экспериментов включается в работу один из описанных базовых непрямых алгоритмов оптимизации. [13]
Проблема выбора шагового множителя pv и генерации плана эксперимента Х решается так же, как в квазиградиентном непрямом алгоритме оптимизации. В качестве критерия останова используется тот же критерий, что и в квазиградиентном непрямом алгоритме оптимизации. [14]
Страницы: 1