Аргана

Cтраница 1

Аргана я французских математиков) геометрическое представление мнимых чисел, воспользовался выражением двукратно протяженная величина ( ( I), стр. [1]

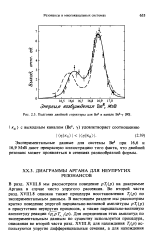Подгонки двойной структуры для Be8 в канале Ве - 7. [2]

Аргана в случае чисто упругого рассеяния. [3]

Аргана), согласно ( 61) и ( 62), есть окружность с радиусом, зависящим от ] t ( рис. 16, а), и с максимумом ( 0, / max) при 1 я / 2 в резонансе. [4]

Весселя и Аргана не обратили внимания, и лишь в 1831 г., когда тот же способ был развит великим математиком Гауссом ( Германия), он стал всеобщим достоянием. [5]

Вектор - одно из фундаментальных понятий современной математики и широко используется в различных ее областях. Аргана и К - Ф - Гаусса по теории комплексных чисел установлена связь между арифметическими операциями над комплексными числами и геометрическими операциями над векторами в двумерном пространстве. Мебиуса понятие вектора нашло широкое применение при изучении свойств трехмерного и многомерного пространств. [6]

В этой главе мы рассмотрим резонансы в процессах рассеяния из начального состояния в несколько конечных состояний, когда внутренние квантовые числа резонансов в общем случае отличаются от квантовых чисел начального и конечного состояний. Аргана для неупругих резонансов. [7]

D Alembert, 1747), но первое строгое доказательство этого факта принадлежит К. Аргана, вошло в обиход после опубликования в 1806 и 1814 работы Ж. Р. Аргана ( J. R. Argand), повторявшей в основном независимо выводы К. [8]

Даламбера и Эйлера, постепенно применяется все большим числом математиков. Этому же вопросу посвящена работа Ж - Аргана, вышедшая в 1806 г. Работа Весселя Об аналитическом представлении направлений содержит полное геометрическое построение теории комплексных чисел, рассматриваемых как векторы плоскости. Хотя в своей работе Вессель стремился главным образом к решению ряда практических задач геодезии и землемерия, он упоминает, что применяемым им исчислением удается не только избегать всех невозможных операций, но и удается объяснить те парадоксы, когда по необходимости прибегают по нескольку раз к невозможному для отыскания возможного. Под невозможными операциями Вессель понимает операции с комплексными числами. [9]

Впервые строгое доказательство основной теоремы было предложено Гауссом в 1779 г. С тех пор появилось много вариантов доказательства, различающихся между собой, так сказать, степенью алгебраичности. Необходимость опираться на свойства непрерывности полей R и С ( иначе, на их топологию) проявляется в той или иной форме; есть даже совсем не алгебраическое и очень короткое доказательство, основывающееся на довольно глубоком понятии аналитической функции комплексной переменной. Сейчас будет приведено доказательство, основанное на элементарных сведениях из математического анализа и восходящее к идеям Даламбера, Эйлера, Гаусса, Коши, Аргана. [10]

Впервые строгое доказательство основной теоремы было предложено Гауссом в 1779 г. С тех пор явилось много вариантов доказательства, различающихся между собой, так сказать, степенью алгебраич-ности. Необходимость опираться на свойства непрерывности полей R и С ( иначе: на их топологию) проявляется в той или иной форме; есть даже совсем не алгебраическое и совсем короткое доказательство, основывающееся на довольно глубоком понятии аналитической функции комплексной переменной. Сейчас будет приведено доказательство, основанное на элементарных сведениях из математического анализа и восходящее к идеям Даламбера, Эйлера, Гаусса, Коши, Аргана. [11]

Но на работы Весселя и Аргана - не обратили внимания, и лишь в 1831 г., когда тот же способ был развит великим математиком Гауссом ( Германия), он стал всеобщим достоянием. [12]

Задача о выражении корней степени п из данного числа была в основном решена в работах А. Аламбер ( 1747), но первое строгое доказательство этого факта принадлежит К. Карно, но в употребление термин вошел после работ К. Аргана, повторявшей в основном независимо выводы К. [13]

Но на работы Весселя и Аргана не обратили внимания, и лишь в 1831 г., когда тот же способ был развит великим математиком Гауссом ( Германия), он стал всеобщим достоянием. [14]

Страницы: 1