Комбинация - поворот
Cтраница 1
Комбинация поворота с трансляцией вдоль оси создает подобие винтового движения. Поэтому подобные комбинации называются винто-ыми осями. Как и винты, винтовые оси могут быть правыми и левыми. [2]
Этот оператор соответствует комбинации поворота па угол л вокруг оси 2 в изотопическом пространстве с операцией зарядового сопряжения. [3]
Линейное отображение (1.1) является комбинацией поворота и подобия ( если А. Коэффициент подобия равен А, а угол поворота равен argA Преобразования подобия и поворота сохраняют форму фигур. [4]
Каждый из трех видов указанных проекций получается комбинацией поворотов, за которой следует параллельное проектирование. [5]
Координата Si дана в декартовых составляющих смещений и представляет собол комбинацию поворотов вокруг связей. [6]
 |
К выводу принципа возможной работы. [7] |
Твердому телу можно придать возможное перемещение, состоящее из переноса в произвольном направлении, поворота относительно произвольной оси или комбинации поворота и переноса. Во всех случаях возможная работа, совершаемая силами, будет равна нулю, если тело находится в равновесии. [8]
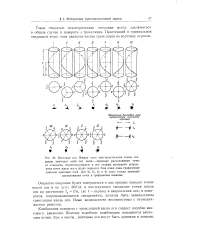
Операциями точечной симметрии являются: повороты вокруг оси симметрии порядка N на угол, равный 360 / Я ( рис. 2, а); отражение в плоскости симметрии m ( зерна л ь н о е Отражение, рис. 2, б); и н в е р с и я 1 ( симметрия относительно точки, рис. 2, в); инверсионные повороты ( комбинация поворота на угол 360 / с одноврем. [10]
Такое умножение возможно и для различных типов преобразования симметрии. Например, комбинация поворота и отражения в плоскости, перпендикулярной оси, приводит к зеркально-поворотным осям n - го порядка. [11]
У полиизобутилена регулярное чередование незамещенных и дважды замещенных углеродных атомов вызывает сильное перекрывание боковых метальных радикалов. Эти стерические помехи не удается устранить никакими комбинациями поворотов вокруг связей, сводящимися к транс - или гош-положениям. Связи в этой молекуле, следовательно, обладают весьма специфической потенциальной функцией, никак не похожей на потенциал с тройной симметрией, описывающий внутреннее вращение в полиэтилене и других цепных молекулах с углеродным скелетом. Можно показать, что полиизобутилен приобретает в результате спиральную структуру, которая возникает при повороте каждой связи на 82 от транс-положения. Регулярно организованная структура возникает в тех случаях, когда направление, или знак поворота одинаковы для каждой связи, а статистически неупорядоченная - когда знак вращения у разных связей различен. [12]
Всякая подгруппа ортогональной группы называется точечной группой. В теории молекул и кристаллов получили применение конечные точечные группы, элементы которых состоят из комбинаций поворотов на определенные углы и отражений в плоскости. Классификация точечных групп приводится в § 3 этой главы. [13]
Про фигуру говорят, что она обладает инверсионной осью ( символ п) порядка п, если совмещение всех ее точек с эквивалентными происходит в два приема: поворотом на угол 360 / я и инверсией. Таким образом, фигура, обладающая инверсионной осью, имеет не только особую линию, но и особую точку. Инверсионная ось является неразрывной комбинацией поворота вокруг оси и инверсии. [15]
Страницы: 1 2