Линейная комбинация - определитель
Cтраница 1
Линейная комбинация определителей необходима для некоторых спиновых состояний ( см. V.4) ив случаях, когда учитывается конфигурационное взаимодействие. [1]
Линейная комбинация определителей необходима для некоторых спиновых состояний ( см. V.4) и в случаях, когда учитывается конфигурационное взаимодействие. [2]
Кроме того, никакая другая линейная комбинация определителей от D, до D8 не имеет такого собственного значения. [3]
В тех случах, когда волновая функция всей системы представляется в виде линейной комбинации слейтеровских определителей, возникает задача вычисления матричных элементов одночастичных и двухчастичных операторов между двумя слейтеровскими определителями. [4]
Требование, связанное с группой симметрии ядерного остова, приводит в общем случае к необходимости строить линейные комбинации определителей D, обладающие необходимой симметрией. Однако для основного состояния подавляющего большинства молекул и всех неметаллических кристаллов задача упрощается тем, что соответствующая точная электронная волновая функция преобразуется по тождественному представлению группы симметрии ядерного остова и соответствует нулевому значению полного спина электронной подсистемы. Разделение спиновых и пространственных координат возможно, если в операторе энергии учитываются лишь электростатические взаимодействия. [5]
ХНП рядом авторов были использованы так шзываемые одноцентровые волновые функции. Такие функции троятся в виде линейной комбинации определителей, содержащих фбитали, центрированные на одном центре, для молекул ХНП - итерированные на ядре атома X. Это облегчает вычисление инте - ралов, встречающихся в ходе расчета. [6]
 |
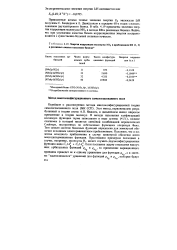
Сопоставление результатов расчета электронного строения КМпО4 различными методами. [7] |
Вторая особенность применения метода МО к комплексным соединениям состоит в том, что при наличии неспаренных электронов энергетическое состояние частицы ( терм - см. гл. V) зача - стую производится от нескольких электронных конфигураций, что требует представления Ф в виде линейной комбинации определителей. [8]
 |
Энергия корреляции молекулы МН3 в приближении KB ( 1 2 в различных сжатых гауссовых базисах. [9] |
Этот метод, первоначально разработанный в теории атома А.П. Юцисом, в дальнейшем нашел широкое применение в теории молекул. В методе наложения конфигураций волновую функцию терма записывают в виде суммы (4.51), каждое слагаемое в которой является линейной комбинацией определителей Слейтера, построенных на собственных функциях оператора Фока. Тем самым система базисных функций определена для замкнутой оболочки исходным однотерминантным приближением. Положим, что в качестве исходного приближения в случае замкнутой оболочки взята многодетерминантная функция. [10]
Поэтому совокупность таких детерминантов образует базис конфигурации. Поскольку в этом представлении оболочка распадается на две подоболочки, отвечающие двум возможным значениям /: / / / 2 и / - / - / 2, все определители, построенные из одноэлектронных функций фп. Совокупность линейных комбинаций определителей, принадлежащих одному классу, образует некоторое подпространство конфигурации, которое называется подконфигурацией. [11]
В самосогласованных расчетах по методу МО ЛКАО межэлектронное взаимодействие учитывается неявно при самосо-гласованни по заряду и в явной форме при самосогласовании по матрице плотности. При этом, очевидно, последовательный расчет энергий переходов требует раздельного самосогласованного расчета всей системы в основном и возбужденных состояниях. В рамках этого приближения многоэлектронная волновая функция возбужденного состояния, соответствующая определенному полному спину, строится в виде линейной комбинации определителей, в которых верхняя занятая МО заменяется виртуальными ( вакантными), полученными при расчете основного состояния. Таким образом удается избежать расчета веей системы в возбужденном состоянии. [12]
Представления индивидуальных квантовых чисел просты. Диагона-лизация секулярной матрицы дает сразу все уровни конфигурации. Однако неполный учет сферической симметрии атома ограничивает сложность конфигураций, которые могут быть исследованы. Приходится дополнительно решать задачу их идентификации. Щг-представления свободны от этих недостатков. Однако собственные функции оператора J2 представляют собой сложные линейные комбинации определителей. Работа с такими базисными функциями требует специального математического аппарата. [13]
Страницы: 1