Неотрицательный корень

Cтраница 1

Неотрицательный корень n - й степени из неотрицательного числа называется арифметическим корнем. Можно доказать, что арифметический корень любой натуральной степени из любого положительного числа существует. [1]

Неотрицательные корни уравнений Х ( ю) 0 и У ( ш) 0 перемежаются. Это говорит о том, что кривая Михайлова последовательно проходит пять квадрантов. [2]

Неотрицательные корни уравнений X ( о) 0 и К ( а) 0 перемежаются. Это говорит о том, что кривая Михайлова последовательно проходит пять квадрантов. [3]

Берем только неотрицательные корни этих уравнений, ибо строится половина годографа Михайлова, соответствующая изменению параметра ц от 0 до оо. [4]

Это позволяет искать лишь неотрицательные корни. [5]

Вместе с (19.4) формула (19.5) дает квадратное уравнение относительно 5Мл, у которого надо выбирать неотрицательный корень. [6]

Графики функций / ( s, ее n - кратной итерации / n ( s и предельной функции q ( s в общем случае. А и С - устойчивые корни, В - неустойчивый. Начальные точки si и 82 попадают в область притяжения корня А, точка зз - область притяжения корня С. [7]

Этот корень равен 1, если га 1; если га т 1, то это единственный неотрицательный корень. [8]

Исходное уравнение имеет решение тогда и только тогда, когда уравнение () имеет хотя бы один неотрицательный корень. [9]

Если функцию у х2 рассматривать только на промежутке х О, то она будет иметь обратную у - л [ х, так как уравнение х 2 - у при у О имеет только один неотрицательный корень. [10]

Поэтому достаточно найти лишь неотрицательные корни. [11]

Если в качестве X выбрать корни уравнения (1.14), т.е. положить Хал, то второе слагаемое в (1.21) с учетом (1.14) станет равным нулю и тогда из (1.21) сразу следует (1.17), т.е. первая часть теоремы доказана. Если же используется граничное условие второго рода то, как указывалось выше, в качестве параметра преобразования Я, следует выбирать неотрицательные корни уравнения (1.15)), т.е. положить А. [12]

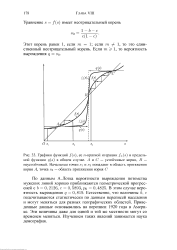
Ои, пройдет п квадрантов плоскости uOv, поочередно пересекая при этом оси Ov и Ои. Так как каждому пересечению оси Ои соответствует корень многочлена v ( JJL), а каждому пересечению оси Ov - корень многочлена ы ( ( л), то, записав все неотрицательные корни многочленов (3.69) в порядке их возрастания, обнаружим при этом, что за каждым корнем многочлена и ( ц) будет следовать корень многочлена к ( ц), и наоборот. [13]

Страницы: 1