Надежность - уравнение
Cтраница 1
Надежность уравнения (V.12) была показана в очень тщательных опытах Вейсца и Гудвина, проведенных в дифференциальном реакторе при 700 С. Теоретическая зависимость, связывающая выгорание кокса со временем, очень хорошо совпадает с экспериментальными данными в изученном диапазоне продолжительности регенерации. В качестве меры скорости реакции было выбрано время выгорания 85 % исходного кокса. При постоянном начальном содержании кокса время выгорания 85 % кокса изменяется пропорционально квадрату диаметра гранулы в диапазоне 3 - 5 мм. Эти факты согласуются с теорией. [1]
Несмотря на кажущуюся надежность уравнения регрессии для всей выборочной совокупности НГДУ, использовать его для практических целей нельзя, так как проверка на нормальность распределения у показала, что р1 043 значительно больше табличного значения, что свидетельствует о ненормальном распределении у. Поэтому необходимо рассмотреть вопрос о правомерности использования данной совокупности НГДУ для корреляционного и регрессионного анализа. Для этого проведено попарное сравнение дисперсий о2 отдельных групп НГДУ. [2]
 |
Коэффициенты эластичности и бетта-коэффициенты. [3] |
Для того чтобы убедиться в надежности уравнения связи и правомерности его использования для практической цели, необходимо дать статистическую оценку надежности показателей связи. [4]
Необходимо подчеркнуть, что проверкой надежности уравнения ( I, 91) в каждом конкретном случае может служить характер расположения точек на GU - С / - прямой. [5]
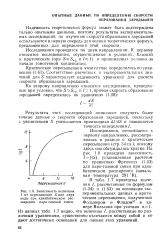 |
Зависимость величины / от пересыщения S для пара воды при адиабатическом расширении паро-газовой смеси. [6] |
Соответствие расчетных и экспериментальных значений для S характеризует надежность уравнений для расчета скорости образования зародышей. [7]
 |
Скорость образования зародышей, установленная по экспериментальным данным для SKp. [8] |
Соответствие расчетных и экспериментальных значений для S характеризует надежность уравнений для расчета скорости образования зародышей. Исследования, относящиеся к этому направлению, были рассмотрены ранее ( стр. [9]
Для расчета малых степеней ионных ассоциаций по любому из этих уравнений необходима самая высокая точность экспериментальных результатов и высокая степень надежности уравнений. [10]
Требования, предъявляемые к явному выражению для функции Т, могут быть весьма различны - они определяются спецификой изучаемого процесса. Так, иногда достаточно найти лишь приближенный вид зависимости функции W от ее аргументов. В то же время при изучении ряда процессов, протекающих при повышенном давлении, требования, предъявляемые к точности и надежности уравнения (2.1.1), весьма жестки. В некоторых случаях необходимо также знать зависимость функции W от параметров, характеризующих структуру системы. [11]
Построенное таким путем уравнение состояния проверяется сопоставлением с экспериментом. Следует, однако, заметить, что для плотной высокотемпературной плазмы экспериментальных данных сравнительно мало и они не дают достаточно полного представления о надежности описания поведения вещества конкретным уравнением состояния. Оценить точность получаемого и применяемого на практике уравнения состояния в широкой области изменения температуры и плотности возможно лишь на основе последовательных теоретических расчетов по моделям различной степени точности. Согласие с экспериментом является при этом необходимым, но недостаточным условием надежности уравнения состояния из-за невозможности экспериментальной проверки во всей области применения. [12]
В связи с этим примером отметим следующее. Хотя из двух уравнений, содержащих общее свойство, легко получить третье уравнение, подобное первым двум, однако надежность - последнего может быть самой различной. Если же эти уравнения не точны, то будут возможны различные варианты. Так, может оказаться, что уравнение ( II, 78) плохо воспроизводит опытный материал. Следовательно, судить о надежности уравнений ( II, 76), ( II, 77) и ( II, 78) по точности одного из них в общем случае не представляется возможным. [13]
Уравнение РК применимо к широкому ряду углеводородов и неуглеводородов, но оно не рекомендуется для полярных компонентов, таких как сероводород, оксид и диоксид азота. Уравнение в первоначальном виде недостаточно точно описывает состояние смесей и становится неточным для индивидуальных углеводородов при условиях, приближающихся к критической точке. Некоторые из модификаций, повышающих точность и надежность уравнения, рассматриваются ниже. [14]
Вызвано это тем, что при составлении чисто эмпирических уравнений форма уравнения выбирается произвольно. Между тем одни и те же экспериментальные данные ( например, по термическим свойствам) могут быть в пределах погрешности эксперимента описаны несколькими уравнениями различного вида. При экстраполяции по этим уравнениям за пределы области эксперимента будут получены значительно отличающиеся один от другого результаты. Да и внутри области эксперимента производные ( особенно вторые), вычисленные по различным уравнениям, будут иметь разное значение и даже знак, что свидетельствует о том, что погрешность при вычислении калорических величин может быть большой. Поэтому для составления более или менее удовлетворительного эмпирического уравнения состояния необходимо иметь данные высокой точности в большом диапазоне температур и давлений, так как в этом случае взаимная увязка данных по различным пересекающимся линиям ( например, по изотермам и изобарам) позволяет повысить надежность уравнения. [15]
Страницы: 1 2