Анализ - динамика - система
Cтраница 1
Анализ динамики системы, использующей гравитационно-градиентный и гироскопический принципы стабилизации. [1]
Как показал анализ динамики системы, для обеспечения требуемой устойчивости можно использовать вязкий демпфер, соединенный с плоским золотником. [2]
Описанный метод анализа динамики систем был применен автором в работе [6] при исследовании параметрических эффектов в измерительных системах. [3]
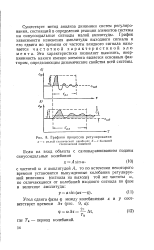 |
Графики процессов регулирования. [4] |
Существует метод анализа динамики систем регулирования, состоящий в определении реакции элементов системы на синусоидальные сигналы малой амплитуды. График зависимости изменения амплитуды выходного сигнала и его сдвига во времени от частоты входного сигнала называется частотной характеристикой элемента. Эта характеристика позволяет выяснить, инерционность какого именно элемента является основным фактором, определяющим динамические свойства всей системы. [5]
Наряду с рассмотренной расчетной схемой для анализа динамики систем, при одновременном действии гармонического и нормального случайного сигналов, может быть использована более простая схема, основанная на введении только одного коэффициента статистической линеаризации, одинакового и для случайной, и для гармонической компонент. [6]
Это решение не представляет интереса для анализа динамики систем регулирования, но может оказаться полезным при расчетах различных предохранительных и аварийных сервоустройств. [7]
Другим типом упрощения, применяемым при анализе динамики систем, является метод уподобления сложной системы другой, более простой. Если из двух постоянных времени в системе одна во много раз больше другой, то влияние первой и будет в основном определять реакцию системы, так что второй можно пренебречь и описать систему уравнением первого порядка. Реакция любой системы с большим количеством постоянных времени не отличается по форме от реакции системы с двумя постоянными времени, что открывает возможности упрощения уравнений. [8]
Для решения любой задачи, связанной с анализом динамики системы автоматического регулирования, необходимо прежде всего составить дифференциальные уравнения ее звеньев. Дифференциальное уравнение каждого звена составляется на основании того физического закбна, который определяет протекающий в данном звена процесс. [9]
 |
Статические характеристики устойчивых элементов. [10] |
Для решения любой задачи, связанной с анализом динамики систем автоматического регулирования, необходимо прежде всего располагать дифференциальным уравнением исследуемой системы. [11]
Одно из важных свойств корневого метода при анализе динамики систем управления состоит в том, что характеристика во временной области определяется только на основании заданных параметров системы. В действительности характер реакции системы может быть точно установлен даже без вычисления выражения для полного решения во времени. Необходимо знать только расположение корней характеристического уравнения на плоскости s, что можно точно определить прежде всего по корневому методу. Это прямо противоположно частотному методу, когда динамическая характеристика во временной области обычно аппроксимируется через предельные значения, например, предельный угол сдвига фаз и критический коэффициент усиления. Хотя корневой метод дает более точное описание переходного процесса, следует заметить, что это делается не за счет уменьшения информации о частотной характеристике. [12]
Из сказанного следует, что использование электронных решающих устройств значительно облегчает анализ динамики систем автоматического регулирования и управления, особенно если схему набора составлять, моделируя отдельные звенья структурной схемы. В этом случае можно изменять схему набора только одного звена ( например, меняя коэффициент усиления регулятора), не нарушая набор остальных звеньев. [13]
Асимптотическое поведение и оценки решений монотонных разностных уравнений / / В кн.: Метод функций Ляпунова в анализе динамики систем. [14]
С ам с о н о в, Белецкая Н.В. К задаче об устойчиости относительного равновесия твердого тела с упругими штангами / / Метод функций Ляпунова в анализе динамики систем. [15]
Страницы: 1 2