Анализ - сложность - алгоритм
Cтраница 1
Анализ сложности алгоритма может быть двух типов: анализ в худшем случае и анализ в среднем случае. [1]
Анализ сложности алгоритма ОБОЛОЧКА-МНОГОУГОЛЬНИКА не вызывает затруднений. Обработка каждой вершины многоугольника осуществляется за постоянное время. При построении опорной прямой в цикле while ( строка 14) на каждую операцию удаления затрачивается постоянное время. [2]
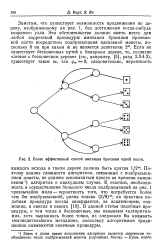 |
Более эффективный способ имитации бросания одной кости. [3] |
Поэтому анализ сложности алгоритмов, связанных с подбрасыва-нием монеты, не должен основываться просто на времени выполнения 1) алгоритма в наихудшем случае. В данной статье подобные процедуры, в том числе и бесконечные, мы называем алгоритмами, хотя выражаясь более точно, их следовало бы называть вычислительными методами, поскольку алгоритмами традиционно называются конечные процедуры. [4]
В результате анализа сложности алгоритма мы получаем асимптотическую оценку ( или порядок алгоритма см. 1.4.1. основного текста) для количества задаваемых им операций. Зная такие оценки для разных алгоритмов решения определенной задачи, мы получаем возможность сравнить эти алгоритмы с точки зрения их эффективности. Однако асимптотические оценки указывают не более чем порядок функции, и результаты сравнения будут справедливы только при очень больших размерах входа. [5]
 |
Определение расположения прямой. - д. [6] |
Мы будем рассматривать анализ сложности алгоритмов только в худшем случае, если не оговорено что-либо иное. [7]
Требования к экономичности таких представлений ставят следующую проблему: на какие фундаментальные вопросы о группах ответы могут быть получены за полиномиальное время. Однако работы по анализу сложности алгоритмов появились относительно недавно. [8]
Для сравнения эффективности алгоритмов при реальных размерах входа и прогнозирования времени выполнения их программных реализаций необходимо знание о точном количестве операций - функций трудоемкости исследуемых алгоритмов. Получение функции трудоемкости требует, очевидно, больших усилий, чем анализ сложности алгоритма. Тем не менее, эти усилия окупаются получением такой информации, которая позволяет проводить практически значимый сравнительный анализ алгоритмов. В этом смысле позволим себе не согласиться с Дж. Макконел-лом, - Точное знание количества операций, выполненных алгоритмом, не играет существенной роли в анализе алгоритмов ( стр. [9]
Предлагаемая методика опирается на введенные элементарные операции процедурного языка высокого уровня, методику анализа алгоритмических конструкций и известные методы анализа алгоритмов. Описания различных методов анализа алгоритмов содержатся в целом ряде литературных источников ( [2, 3, 4, 5]), посвященных анализу сложности алгоритмов, в частности и в основном тексте книги. [10]
Если в действительности число вершин выпуклой оболочки равно h, то время выполнения алгоритма Джарвиса будет 0 ( hN), и он очень эффективен, когда заранее известно, что значение h мало. Например, если оболочка заданного множества является многоугольником с произвольным постоянным числом сторон, то ее можно найти за линейное относительно числа точек время. Этот факт чрезвычайно важен в свете анализа сложности алгоритмов построения выпуклой оболочки в среднем, который будет представлен в следующей главе. [12]
Страницы: 1
