Модельная задача
Cтраница 1
Модельная задача, используемая для методических целей, представляет собой исследование набора альтернативных механизмов, один из которых принимается за истинный. Казалось бы, в ситуации, когда истинный механизм и константы скоростей всех стадий известны, решать нечего - что заложили, то и получили. Расчет по истинному механизму является математическим аналогом физико-химического эксперимента. В результате него получаются кинетические данные, в наигем случае - зависимости концентраций различных продуктов от времени. Задача же состоит в том, чтобы, используя общие контрольные требования и формулируемые в данном случае на основании математического эксперимента частные контрольные требования, уверенно отсечь все механизмы, альтернативные истинному. Кроме того, расчет, в котором используется метод оврагов Гельфанда - Цейтлина, при обработке данных математического эксперимента по истинному механизму должен показать эффективность упомянутой математической методики применительно к решению задач химической кинетики, приводя к истинным значениям констант, даже если в начале расчета взяты их испорченные значения. Выяснив, какие именно цели могут быть достигнуты при решении модельной задачи, сформулируем теперь те требования, которым она должна удовлетворять. [1]
Модельные задачи, описанные в гл. [2]
Модельная задача о поведении цепочки с исключенным объемом в тонком капилляре или плоской щели позволяет ознакомиться с простейшей формой применения концепции скейлинга и понятия блоба. [3]
Модельные задачи о движении тела в среде с сопротивлением представляют собой обобщение аналогичной задачи динамики материальной точки. Они позволяют выявить и изучить типовые закономерности взаимодействия между поступательным и вращательным движением тела. [4]
Данная модельная задача вполне аналогична задаче о точечном заряде, находящемся в состоянии покоя над шварц-шильдовской дырой, которая была рассмотрена в разд. В задаче о точечном заряде можно было не думать о механизме подвешивания заряда ( нить или нечто другое), поскольку такой подвес мог быть в принципе электрически нейтральным и иметь вакуумную диэлектрическую проницаемость, а следовательно, мог не оказывать влияния на электромагнитное поле. Иначе обстоит дело с гравитационным полем. Механизм подвешивания ( нити) должен оказывать усилие на подвешенные массы; таким образом, в нем должны возникать внутренние напряжения, а эти напряжения будут создавать гравитационные силы. Более того, уравнения поля, предложенные Эйнштейном и описывающие создание гравитации массой, моментом и напряжением, заключают в себе уравнения движения и баланса сил для любых создающих гравитацию объектов ( см., например, разд. [5]
Модельной задачей, иллюстрирующей подход, связанный с методом граничных функционалов, является проблема нахождения числа независимых множеств в двудольных графах. [6]
Рассматриваемая модельная задача представляет собой часть описанной в гл. Здесь будет рассмотрена только частная задача - нахождение наилучшей стратегии для определения местоположения источника утечки вещества, обнаруженного в реке ( см. гл. Предполагается, что цель задачи состоит в том, чтобы обеспечить помощь должностному лицу, возможно не обладающему достаточным опытом и находящемуся на дежурстве после окончания рабочего дня. [7]
Эта модельная задача является иллюстрацией сложного граничного слоя, возникающего в динамических ситуациях вблизи истинного горизонта, и демонстрирует, как можно исключить этот слой из рассмотрения, растягивая горизонт. После этого в подразд. Эта задача помогает понять, что такое поверхностный ток и омические потери на горизонте, и наглядно показывает мощь мембранного подхода в исследовании электродинамических процессов вокруг черных дыр. Эта задача позволит нам оценить силу Лоренца, действующую на заряды и токи на растянутом горизонте, а также выяснить, какую роль играет первое начало термодинамики в качестве закона, определяющего поток энергии и углового момента в черную дыру. Эта задача демонстрирует плодотворность риндлеровского приближения и позволяет разобраться в динамике электрических и магнитных полей, движущихся относительно горизонта. Это обсуждение понадобится нам позднее ( см. разд. B ниже), когда мы рассмотрим выглаживание хаотического магнитного поля горизонтом черной дыры. [8]
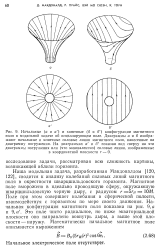
Наша модельная задача, разработанная Макдоналдом [120, 122], сводится к анализу колебаний силовых линий магнитного поля в окрестности шварцшильдовского горизонта. Магнитное поле вморожено в идеально проводящую сферу, окружающую шварцшильдовскую черную дыру, с радиусом г 5гн ЮМ. Поле при этом совершает колебания в сферической полости, взаимодействуя с горизонтом по мере своего движения. Это поле чисто радиальное, но ниже экваториальной плоскости оно направлено вовнутрь дыры, а выше этой плоскости - наружу. [10]
Эта модельная задача является хорошим примером перескока новых опоронов на растянутый горизонт, рассмотренного в разд. Наш формализм теории возмущений становится неприменимым, если когда-либо будет достигнут этот режим, 9 / / - 2 § н, но этот формализм остается в силе почти вплоть до самого наступления этого режима и поэтому может обеспечить критерий по порядку величины для перескока новых опоронов на растянутый горизонт. [11]
Наша первая модельная задача дает представление о медленно ( квазистатически) изменяющихся гравитационных возмущениях невращающейся дыры. Рассмотрим невращающуюся невозмущенную ( шварцшильдовскую) черную дыру с массой М и радиусом горизонта Гн ЪМ. [12]
Для модельных задач справедливы формулы, выражающие их решения в интегральной форме с помощью фундаментальных матриц решений, ядер Пуассона и однородной матрицы Грина. [13]
Для модельной задачи о контакте двух прямоугольников, в одном из которых имеется длинная неглубокая ступенчатая выемка, даются сравнения решений МГИУ, МКЭ и экпериментальных данных, подчеркивающие точность результатов, полученных МГИУ. [14]
 |
Плановое расположение наблюдательных скважин по схеме креста ( заштрихован расчетный блок. [15] |
Страницы: 1 2 3 4