Точное значение - вероятность
Cтраница 1
Точные значения вероятностей Pi, соответствующих различным значениям дискретного параметра или различным интервалам ряда распределения непрерывного параметра, нам никогда не известны. Поэтому точное значение энтропии не может быть найдено. Фактически мы всегда будем располагать оценкой энтропии Н [ х ] п по некоторой совокупности п наблюдений. [1]
Сравнить точное значение вероятности Р 1 1 1 А с оценкой, полученной по неравенству Чебышева. [2]
Данное предположение позволяет получить точные значения вероятности принадлежности к данному классу и критерия значимости. [3]
Критерий Фишера позволяет получить точные значения вероятности событий, столь же или еще менее вероятных, чем те, которые в действительности наблюдались. Этот критерий особенно полезен при малых значениях N. Однако в общем случае связанные с ним вычислительные процедуры являются достаточно сложными и трудоемкими. [4]
Выведите формулы, позволяющие достаточно эффективно вычислять точное значение вероятности того, что Х 2 % k i Xk Для линейной конгруэнтной последовательности с максимальным периодом. [5]
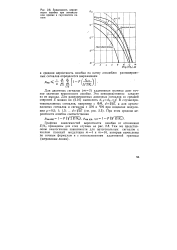 |
Зависимость вероятности ошибки при оптималь - ош ном приеме в гауссовском канале. [6] |
Для двоичных сигналов ( т 2) аддитивная граница дает точное значение вероятности ошибки. Это непосредственно следует из ее вывода. [7]
Критическое значение: критическое значение не используется, поскольку путем перебора мы получим точное значение вероятности. [8]
Мы видим, что верхняя граница Чернова отличается примерно на 6 дБ от точных значений вероятности ошибки при L l, но по мере роста L она становится плотнее. [9]
Критическое значение: критическое значение не используется, поскольку с помощью перебора мы получим точное значение вероятности. [10]
В частности, как будет видно из дальнейшего, в случаях прямоугольной ямы и точного резонанса при этом получаются точные значения вероятностей перехода. [11]
В том случае, когда ошибки 6j подчиняются нормальному распределению ( такое поведение ошибок особенно часто встречается на практике), можно найти точное значение вероятности, с к-рой абс. [12]
Мы займемся здесь вычислением вероятностей принятия решения dj или d2 и расчетом средней стоимости выбора для последовательной процедуры, определенной посредством соотношения ( 11) § 12.14. Хотя в большинстве задач точные значения вероятностей принятия решения d4 или dz найти и не удается, существуют простые приближенные формулы. [13]
При этом число п должно быть достаточно велико. Точное значение вероятности соответствует п оо, однако уже при контроле десятков и сотен изделий получается величина Р, достаточно близкая к вероятности. [14]
Теперь обратим наше внимание на характеристику качества этих кодов. Во-первых, точное значение вероятности ошибки кодового слова ( символа) для М - ичного ортогонального кода по каналу с релеевскими замираниями с разнесением было дано в замкнутой форме в разделе 14.4. Как показано раньше, это выражение скорее громоздкое для расчетов, особенно когда L или М или оба параметра большие. Вместо этого мы используем объединенную верхнюю границу, которая очень удобна. [15]
Страницы: 1 2