Конечное значение - величина
Cтраница 1
Конечное значение величины С позволяет сформулировать следующее правило: за любой располагаемый промежуток времени можио добиться либо усвоения учеником большего количества информации, но на более низком уровне обученности, либо меньшего количества информации, но на более высоком Уровне. [1]
Ркон - некоторое конечное значение величины контурного давления рк к моменту окончания эксплуатации газовой залежи. [2]
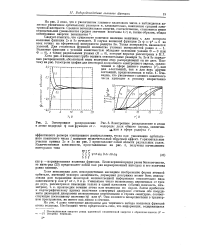 |
Электронное распределение в атоме водорода. ij как функция от г.| Электронное распределение в атоме водорода. доля общего заряда, заключений нал в сфере радиуса г. [3] |
Следует отметить, что существует конечное значение величины г, для которого волновые функции 2s и 3s исчезают. Такая поверхность называется узловой. Волновые функции с угловой зависимостью обладают угловыми узлами 6 0 или Ф 0), а также радиальными узлами ( R 0), которые вкратце рассмотрены в II.7. Хотя рис. 2 и позволяет грубо оценить относительные размеры Is, 2s и 3s зарядовых распределений, абсолютной меры величины этих распределений он не дает. [4]
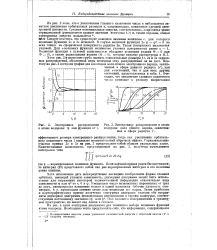 |
Электронное распределение в атоме водорода. i как функция от г.| Электронное распределение в атоме водорода. доля общего заряда, заключенная в сфере радиуса г. [5] |
Ивдо Следует отметить, что существует конечное значение величины г, для которого волновые функции 2s и 3s исчезают. Такая поверхность называется узловой. Волновые функции с угловой зависимостью обладают угловыми узлами 0 0 или Ф 0), а также радиальными узлами ( R - 0), которые вкратце рассмотрены в II.7. Хотя рис. 2 и позволяет грубо оценить относительные размеры Is, 2s и 3s зарядовых распределений, абсолютной меры величины этих распределений он не дает. [6]
Однако при исчезающе малом, но конечном значении величины Dz, граничное условие (10.32) означает, что градиент концентрации в сечении на выходе равен нулю. Это несколько неожиданный вывод, потому что явно превалирующее условие, когда Dz О, не может рассматриваться как предел общего решения задачи при Dz, стремящемся к нулю. Рассмотренная ситуация имеет аналогию в классической механике жидкости, решенную Прандтлем путем введения концепции пограничного слоя. В последнем случае решения задачи невязкого течения или уравнений Эйлера не являются пределом, к которому стремится решение общих уравнений Навье - Стокса, когда вязкость приближается к нулю. [7]
Все другие варианты находятся между этими крайними случаями и имеют конечные значения величин Я и а. Рассмотрим предельные случаи отдельно. [8]
Для того чтобы удовлетворить условию непрерывности, начальные значения должны быть равны соответствующим конечным значениям величин гиг для предыдущего интервала. [9]
Здесь следует отметить, что если всем с ц придать начальные значения оо ( а не 0), то конечное значение величины с ц будет равно весу цепи, проходящей через вершину хг. Легко также видеть, что, исходя из структуры матрицы в, полученной в процессе той итерации, когда элемент с - - становится отрицательным, легко найти цикл отрицательного веса, соответствующий этому элементу. [10]
Поэтому в дальнейших выводах мы его опускаем, однако ладо помнить, в каких случаях он может оказывать влияние яа конечные значения величины поляризации. [11]
 |
Профиль скоростей. [12] |
Из предыдущего известна методика образования критериев подобия, которая в сущности очень проста, так как сводится к нахождению отношения конечных значений величин, входящих в уравнение. Больше трудностей вызывает выбор условий однозначности. В данном случае должны быть заданы геометрическая характеристика, основные физические свойства потока, начальные и граничные условия. [13]
Если каждому значению) переменной величины х, принадлежащему некоторой совокупности ( множеству) Е, соответствует одно и только одно конечное значение величины у, то у называется функцией ( однозначной) от х, или зависимой переменной, определенной на множестве Е; х называется аргументом, или независимой переменной. [14]
Так как в расчетах, приведенных в этой и последующих главах, обычно приходится иметь дело с очень небольшими концентрациями, а исследователя преимущественно интересуют примерные конечные значения величин, получающихся в результате расчетов ( а часто даже порядок величин), то в дальнейшем для упрощения мы будем пользоваться концентрационными формулами. [15]
Страницы: 1 2