Андронова-хопфа
Cтраница 1
Андронова-Хопфа, уравнение Кортевега-де Фриза, с 1895 года дожидавшееся возможностей компьютерной имитации, уравнение Бюргерса щ иих ихх и многие другие. Можно сказать, что на таких моделях стоит почти вся физика. Методы теории бифуркаций ( теорема о центральном многообразии и теория нормальных форм) показывают, что построение таких простых моделей, по крайней мере в некоторых случаях, может быть не только искусством, но и строго обоснованным научным подходом. [1]
Из точки бифуркации Андронова-Хопфа субкрнтически отделяется ветвь неустойчивых периодических решений. С учетом упомянутой симметрии таких точек бифуркации оказывается две1 ( на рис. 5.26 а им отвечает одна точка), и из них ответвляются две ветви периодических решений, траектории которых взаимно симметричны по отношению к оси г. При уменьшении значения параметра г уменьшается расстояние периодических траекторий до состояния равновесия x y - z Q. [2]
На практике часто встречается бифуркация Андронова-Хопфа, в которой фокус теряет устойчивость, и при этом рождается асимптотически устойчивый цикл. Такие системы были описаны в разделе 5.5. В частности, если в правой части системы уравнений (5.15) положить / ( г) - ег - г3, то получается как раз такая бифуркация при прохождении е через нуль. Это, конечно, рояль в кустах - зато максимально просто. [3]
 |
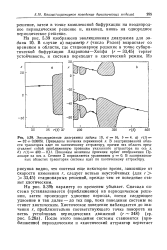
Схематическое изображение перехода через критические точки при квазистационарном поведении. [4] |
Случай d) соответствует бифуркации Андронова-Хопфа на устойчивой ветви стационарных решений. [5]
 |
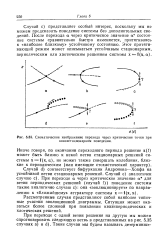
Нарта динамических режимов для системы уравнений, описывающей генератор с инерционной нелинейностью Анищенко-Астахова, и фазовые портреты аттрактора в некоторых характерных точках. [6] |
Момент т - 0 отвечает бифуркации Андронова-Хопфа - рождению предельного цикла. При дальнейшем изменении параметров этот цикл в свою очередь может претерпевать различные бифуркации. [7]
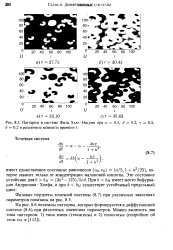 |
Паттерны в системе Фитц Хью-Нагумо при а, 3, - у, 6 в различные моменты времени t. [8] |
При Ь Ьн имеет место бифуркация Андронова-Хопфа, а при Ь Ьц существует устойчивый предельный цикл. [9]
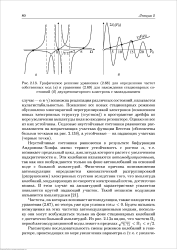 |
Графическое решение уравнения для определения частот собственных мод ( а и уравнения для нахождения стационарных состояний ( б двухрезонаторного клистрона с запаздыванием. [10] |
Неустойчивые состояния равновесия в результате бифуркации Андронова-Хопфа мягко теряют устойчивость с ростом а, т.е. возникает предельный цикл, амплитуда которого растет с увеличением надкритичности а. Эти колебания называются автомодуляционными, так как они возбуждаются только на фоне автоколебаний на основной моде с большой амплитудой. Физически причина возникновения автомодуляции определяется кинематической разгруппировкой ( разрушением) электронных сгустков вследствии того, что амплитуда колебаний, модулирующих по скорости электронный поток, достаточно велика. В этом случае на амплитудной характеристике усилителя появляется крутой падающий участок. [11]
В работе [57] построено УР бифуркации Андронова-Хопфа в общем случае дифференциального уравнения s - ro порядка с фредголь-мовым оператором при старшей производной и наличии жордановых цепочек, доказана теорема о наследовании. [12]
На рис. 5.36 представлены шесть случаев, когда при переходе через точку поворота или точку бифуркации Андронова-Хопфа происходит резкое изменение ( скачок) решения. На рисунках изображены перескоки при увеличении или уменьшении значений параметра со временем. На рис. 5.36 а и 5.36 Ь приведены наиболее типичные случаи так называемого явления гистерезиса. Случай двух петель гистерезиса представлен на рис. 5.36 с. Общим для всех трех случаев является то, что с помощью соответствующих изменений параметра здесь можно получить все устойчивые стационарные решения. [13]
В случае а) параметр г ( число Рэлея) возрастает со временем в области, где стационарное решение в точке субкритической бифуркации Андронова-Хопфа ( г - 33 45) теряет устойчивость, и система переходит в хаотический режим. [15]
Страницы: 1 2