Оценка - математическое ожидание
Cтраница 3
Прямопоказывающий цифровой измеритель оценки математического ожидания стационарного эргодического случайного процесса может быть выполнен на основе трех серийно выпускае-вых приборов: АЦП, генератора импульсов и ЭСЧ. [31]
Следует отметить, что оценка математического ожидания по формуле ( 38) не является оптимальной оценкой величины Q, за исключением случая, когда интегрируется чисто случайный процесс. [32]
Сравнивая доверительные интервалы для оценки математического ожидания видим, что расхождения весьма незначительные, в то время как для среднеквадратичного отклонения приближенный метод дает большую погрешность. [33]
В табл. 2 приведены оценки математического ожидания, дисперсии и среднеквадратичного отклонения концентрации крепкого и слабого газа на 1 линии при работе системы автоматической стабилизации и без нее. [34]
В табл. 1 приведены оценки математического ожидания Е и стандартного отклонения s разности расчетных и экспериментальных значений параметров равновесия жидкость - пар без коррекции перекрестных параметров з и ь - С о), а также при коррекции одного и двух параметров. & г if обозначают соответственно разности между расчетными и экспериментальными значениями мольной доли первого компонента в жидкости, мольной доли первого компонента в паре, коэффициента распределения первого компонента, коэффициента распределения второго компонента, температуры и давления; сокращения н.к. и к.к. соответствуют параметрам точек начала и конца кипения. [35]
Известны также итеративные процедуры оценки математического ожидания и дисперсии при неизвестном е, весьма эффективные для реализации на ЭВМ. [36]
Этим обстоятельством пользуются при оценке математического ожидания случайных величин. [37]
Сложнее обстоит дело с оценкой математических ожиданий и дисперсий дополнительных погрешностей. [38]
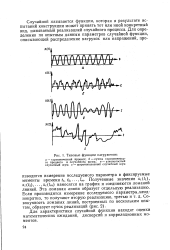 |
Типовые функции нагружения. [39] |
Для характеристики случайной функции находят оценки математических ожиданий, дисперсий и корреляционных моментов. [40]
Таким образом, для нахождения оценки математического ожидания по реализации случайного стационарного процесса выходных параметров комплектующих радиоизделий необходимо знать его корреляционную функцию. [41]
Известно, что в качестве оценок математического ожидания и среднего квадратического отклонения случайной величины X можно принять соответственно выборочную среднюю х и выборочное среднее квадратическое отклонение ав. [42]
В заключение изложим алгоритм построения оценок математического ожидания и автокорреляционной функции фазовых координат с использованием разложения по ортонормированным базисам. [43]
Погрешность этой оценки определяется погрешностью оценок математических ожиданий результатов измерения в первом и втором экспериментах. [44]
X - это значит произвести оценку математического ожидания величины X. При этом, если измеряемая величина X постоянна, то оценка для тх есть приближенное значение истинного значения измеряемой величины, а если измеряемая величина случайная, то оценка для тх есть приближенное значение математического ожидания измеряемой случайной величины. [45]
Страницы: 1 2 3 4