Дисперсионный анализ
Cтраница 3
Дисперсионный анализ табл. 2 и 3 позволил установить, что на значения Ф4 ( а) в среднем существенно влияют параметры / 0, сх и срх. На критерий Ф5 ( а) практически влияли все варьируемые параметры. [31]
Дисперсионный анализ в вычислительном аспекте основан на разложении дисперсии Сто на составляющие, порождаемые независимыми факторами. [32]
Дисперсионный анализ непараметрический - группа статистических методов, позволяющих оценить влияние различных одновременно действующих факторов на случайную величину с непрерывным распределением. Никаких других предположений относительно распределения исследуемой случайной величины не формулируется. [33]
Дисперсионный анализ является начальной стадией исследования и позволяет ответить на вопрос, существуют ли статистические связи между анализируемыми параметрами и целесообразно ли продолжать работу по их изучению. [34]
Дисперсионный анализ предназначен главным образом для выявления степени влияния контролируемых факторов на отклик. В зависимости от количества факторов, включенных в анализ, различают однофакторный, двухфактор-ный и многофакторный дисперсионный анализ. [35]
Дисперсионный анализ, проведенный для 124 объектов с ньютоновской нефтью, позволил установить, что на коэффициент нефтеотдачи существенное влияние оказывают все рассмотренные факторы. [36]
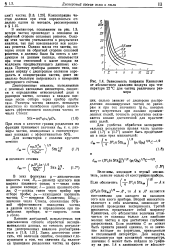 |
Зависимость поправки Кэнингема от абсолютного давления воздуха при температуре 22 С для частиц различного размера. [37] |
Дисперсионные анализы, выполненные с помощью каскадных импакторов, сводятся к определению относительной доли и размеров частиц, осевших в каждом каскаде после отбора через прибор пробы газа. [38]
Дисперсионный анализ показал, что результат учета в сильной степени зависит от того, на каких деревьях, ярусах и в каких квадратах они получены. [39]
Дисперсионный анализ - это математический метод, предназначенный для изучения объектов с факторами качественного типа. Он позволяет разложить общую дисперсию выходной величины на отдельные компоненты, обусловленные влиянием отдельных факторов. При дисперсионном анализе задаются вопросы, влияет ли данный фактор на интересующий нас показатель и какова сила влияния этого фактора. [40]
Дисперсионный анализ состоит в выделении и оценке отдельных факторов, вызывающих изменение изучаемой случайной величины. Для этого суммарная выборочная дисперсия раскладывается на составляющие по независимым факторам. Каждая из этих составляющих представляет собой оценку дисперсии генеральной совокупности. Для определения влияния фактора необходимо оценить значимость соответствующей выборочной дисперсии в сравнении с дисперсией воспроизводимости, обусловленной случайными факторами. Проверка значимости оценок проводится по критерию Фишера. Если рассчитанное значение критерия Фишера окажется меньше табличного, то влияние фактора не значимо. Если же рассчитанное значение критерия Фишера окажется больше табличного, то рассматриваемый фактор влияет на изменчивость средних значений. Предполагается, что случайные ошибки наблюдений имеют нормальное распределение и что факторы влияют только на изменение средних значений, а дисперсия наблюдений постоянна. Если нужно получить нормальное распределение выходной величины, то к случайным факторам желательно относить только те факторы, влияние которых очень мало. [41]
Дисперсионный анализ можно производить, непосредственно измеряя капли ( или частицы) под микроскопом, в окуляр которого вставлена микрометрическая сетка. Каждое деление сетки соответствует определенной длине х объекта, видимого под микроскопом. Пользуясь микрометрической сеткой, подсчитывают число капель ( частиц) одного размера в поле зрения. [42]
Дисперсионный анализ часто применяется совместно с аналитической группировкой ( см. гл. В этом случае данные подразделяются на группы по значениям признака-фактора, вычисляются значения средних величин результативного признака в группах, считается, что различия в их значениях определяются различиями в значениях фактора. Задача состоит в оценке существенности различий между средними значениями результативного признака в группах. Как было показано в предыдущем параграфе, когда выделяются две группы, эта задача решается с помощью / - критерия. Если же число сравниваемых групп больше двух, то существенность различий между группами доказывается с помощью дисперсионного анализа, на основе F-критерия. [43]
Дисперсионный анализ должен проводиться в установленном порядке, если из измерений вязкости не следует, что различные эмульсии будут иметь идентичные средние размеры просто потому, что они приготовляются по одной и той же методике. Это касается случаев, когда сравниваются эмульсии с различными концентрациями дисперсной фазы. [44]
Дисперсионный анализ в основном употребляется для обнаружения углеводородов, получаемых из нефти. [45]
Страницы: 1 2 3 4